Zestaw użytkownika nr 8887_2712
Zestaw użytkownika
nr 8887_2712
Wyrażenie 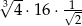 zapisane w postaci potęgi liczby 2, to
zapisane w postaci potęgi liczby 2, to
A) 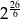 B)
B) 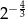 C)
C) 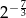 D)
D) 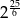
Wartość wyrażenia 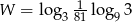 jest równa
jest równa
A) -3,5 B) -8 C) -2 D) -3
Funkcja 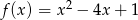 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 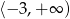 B)
B) 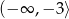 C)
C) 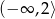 D)
D) 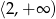
Wiadomo, że 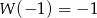 , gdy
, gdy 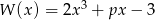 . Zatem wartość współczynnika
. Zatem wartość współczynnika 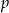 wynosi:
wynosi:
A) -4 B) 4 C) -1 D) 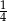
Ciąg arytmetyczny 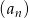 określony jest wzorem
określony jest wzorem 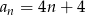 . Zatem suma
. Zatem suma 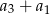 jest równa
jest równa
A) 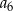 B)
B) 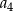 C)
C) 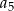 D)
D) 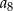
Liczby 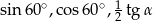 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt  jest kątem ostrym. Zatem jego miara jest równa
jest kątem ostrym. Zatem jego miara jest równa
A) 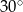 B)
B) 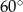 C)
C) 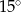 D)
D) 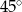
Stosunek miar kątów czworokąta jest równy 1:2:3:4. Zatem najmniejszy kąt tego wielokąta ma miarę
A) 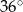 B)
B) 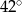 C)
C) 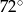 D)
D) 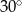
Które z podanych równań jest równaniem prostej.
A) 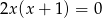 B)
B) 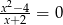 C)
C) 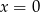 D)
D) 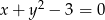
Przekątna graniastosłupa prawidłowego czworokątnego ma długość 10 cm, a krawędź podstawy ma długość 5 cm. Cosinus kąta nachylenia tej przekątnej do podstawy jest równy
A) 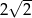 B)
B) 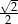 C)
C) 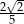 D)
D) 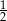
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 20 B) 25 C) 16 D) 30
Liczba, której 4% jest równe 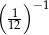 , to
, to
A) 0,12 B) 100 C) 300 D) 0,48
Ile liczb naturalnych należy do zbioru rozwiązań nierówności 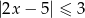 ?
?
A) 4 B) 0 C) 3 D) 2
Zbiorem rozwiązań nierówności 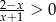 jest
jest
A) 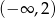 B)
B) 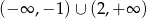 C)
C) 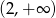 D)
D) 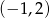
Kod, który zapisany jest na karcie dostępu, składa się z czterech cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się stukrotnie. Ile jeszcze cyfr należy dopisać do kodu?
A) 2 B) 1 C) 6 D) 100
Rozwiązanie równania 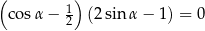 w przedziale
w przedziale 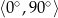 , to
, to
A) 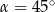 lub
lub 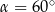
B) 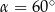 lub
lub 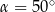
C) 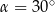 lub
lub 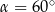
D) 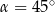 lub
lub 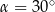
Do wykresu funkcji 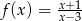 należy punkt
należy punkt
A) 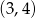 B)
B) 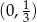 C)
C) 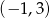 D)
D) 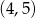
Jeżeli promień podstawy stożka zwiększymy o 20%, a wysokość zmniejszymy o 20%, to objętość stożka
A) zmniejszy się o 4%
B) zwiększy się o 1,52%
C) zwiększy się o 15,2%
D) nie zmieni się
Okrąg opisany na sześciokącie foremnym ma promień 2. Promień okręgu wpisanego w ten sześciokąt jest równy
A) 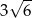 B)
B) 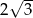 C)
C) 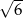 D)
D) 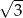
Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 63% B) 45% C) 33% D) 22%
W pewnym liceum 85% uczniów posiada telefony komórkowe. Pozostałych 27 uczniów nie posiada telefonów komórkowych. Wobec tego telefony posiada
A) 154 osoby B) więcej niż 200 osób C) 180 osób D) mniej niż 160 osób
Wskaż równanie okręgu stycznego do osi 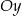 .
.
A) 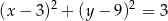
B) 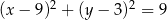
C) 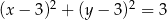
D) 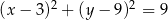
Prosta prostopadła do prostej 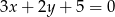 ma równanie:
ma równanie:
A) 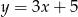 B)
B) 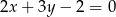 C)
C) 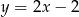 D)
D) 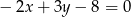
Równanie 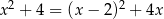
A) ma dokładnie dwa rozwiązania.
B) nie ma rozwiązań
C) ma tylko jedno rozwiązanie
D) spełnia każda liczba rzeczywista
Wymiary prostopadłościanu o objętości 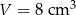 i polu powierzchni całkowitej
i polu powierzchni całkowitej 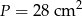 tworzą ciąg geometryczny. Wyznacz długości krawędzi bryły.
tworzą ciąg geometryczny. Wyznacz długości krawędzi bryły.
Rozwiąż równanie: 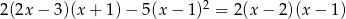 .
.
Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest prostokątem. Przekątna tego prostokąta ma długość 12 i tworzy z bokiem, którego długość jest równa wysokości walca, kąt o mierze 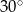 .
.
- Oblicz pole powierzchni bocznej tego walca.
- Sprawdź, czy objętość tego walca jest większa od
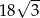 . Odpowiedź uzasadnij.
. Odpowiedź uzasadnij.
W trójkącie ostrokątnym 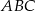 dane są długości boków:
dane są długości boków: 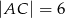 ,
, 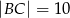 . Pole trójkąta jest równe
. Pole trójkąta jest równe 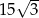 . Oblicz
. Oblicz
- długość boku
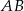 ;
; - sinus kąta
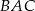 ;
; - pole koła opisanego na trójkącie
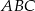 ;
; - długość promienia okręgu wpisanego w trójkąt.
Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 70, a pole 210.
Spośród 5 monet jednozłotowych, 7 dwuzłotowych i 6 pięciozłotowych wybieramy 3 monety. Oblicz prawdopodobieństwo, że wszystkie trzy monety będą miały ten sam nominał.
Oblicz pole i obwód trójkąta o wierzchołkach: 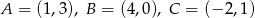 .
.

