Zestaw użytkownika nr 8911_5094

Zestaw użytkownika
nr 8911_5094

Zadanie 1

Tabela przedstawia pewne dane i ich liczebność

Wartość danej	-4	2	4	7	20
Liczebność	7	2	3	6	2

Oblicz średnią arytmetyczną tych danych.
Podaj medianę.
Oblicz odchylenie standardowe.

Zadanie 2

Przeprowadzono badania, dotyczące liczby osób jadących w samochodach osobowych w godzinach rannych, w kierunku centrum pewnego miasta. Wyniki badań przedstawione są na digramie kołowym.

Oblicz średnią liczbę osób jadących w samochodzie osobowym w godzinach rannych w kierunku centrum.
Oblicz prawdopodobieństwo, że w losowo wybranym samochodzie osobowym, w godzinach rannych, w kierunku centrum, były więcej niż 3 osoby.
Wiedząc, że samochodów osobowych, w których były 4 osoby, zaobserwowano o 350 więcej, niż samochodów w których było 5 osób, oblicz, ile wszystkich samochodów obserwowano w trakcie badań.

Zadanie 3

Zważono 150 losowo wybranych kostek masła produkowanego przez pewien zakład mleczarski. Wyniki badań przedstawiono w tabeli.

Masa kostki masła [dag]	Liczba kostek masła
16	1
18	15
19	24
20	68
21	26
22	16

Na podstawie danych przedstawionych w tabeli oblicz średnią arytmetyczną oraz odchylenie standardowe masy kostki masła.

Zadanie 4

Uczniowie napisali pracę kontrolną. 30% uczniów otrzymało piątkę, 40% otrzymało czwórkę, 8 uczniów otrzymało trójkę, a pozostali ocenę dopuszczającą. Średnia ocen wynosiła 3,9. Ilu uczniów otrzymało piątkę?

Zadanie 5

W pewnym liceum, wśród uczniów 30 osobowej klasy (każdy uczeń pochodzi z innej rodziny), zebrano dane na temat posiadanego rodzeństwa. Wyniki badań przedstawiono na diagramie.

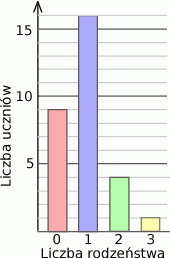
Wychowawczyni wybrała 3 osoby z tej klasy. Oblicz prawdopodobieństwo, że jedna z nich ma dwoje rodzeństwa, a dwie pozostałe nie mają rodzeństwa. Wynik zaokrąglij do części setnych.
Oblicz średnią liczbę dzieci w jednej badanej rodzinie, odchylenie standardowe i medianę.

Zadanie 6

W pewnej szkole przeprowadzono ten sam sprawdzian z matematyki w trzech klasach 1a, 1b i 1c. Na poniższym diagramie przedstawiono wyniki tego sprawdzianu z wyszczególnieniem liczby osób, które uzyskały poszczególne oceny.

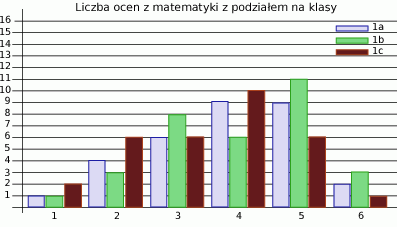
Ilu uczniów pisało sprawdzian w poszczególnych klasach?
Która z ocen była wystawiana najczęściej?
W której klasie średnia ocen ze sprawdzianu była najwyższa?

Zadanie 7

Na podanym wykresie przedstawiono stan wody

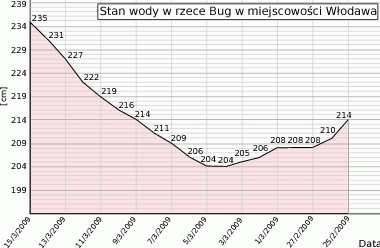
w rzece Bug w okresie od 25 lutego do 15 marca 2009.

W których dniach stan wody w rzece nie przekraczał 207 cm?
Jaki był średni stan wody w rzece w dniach 1-10 marca 2009?
O ile procent podniósł się stan wody w rzece między 6 a 12 marca? Wynik podaj z dokładnością do jednego punktu procentowego.

Zadanie 8

Średnia arytmetyczna liczb: 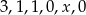3,1,1,0,x,0 jest równa 2. Oblicz .

Zadanie 9

Właściciel kiosku notował liczbę biletów komunikacji miejskiej sprzedanych w kolejnych godzinach. Wyniki obserwacji zapisał w tabeli.

Czas obserwacji	Liczba biletów
5:00–6:00	2
6:00–7:00	3
7:00–8:00	9
8:00–9:00	8
9:00–10:00	6
10:00–11:00	4
11:00–12:00	3
12:00–13:00	3
13:00–14:00	3
14:00–15:00	5
15:00–16:00	8
16:00–17:00	6

Oblicz średnią liczbę biletów sprzedawanych w ciągu 1 godziny.
Wynikiem „typowym” nazywamy wynik, który różni się od średniej o mniej niż jedno odchylenie standardowe. Podaj wszystkie godziny, w których liczba sprzedanych biletów nie była „typowa”.

Zadanie 10

Na diagramie poniżej przedstawiono procentowy podział miesięcznych zarobków w pewnej ﬁrmie.

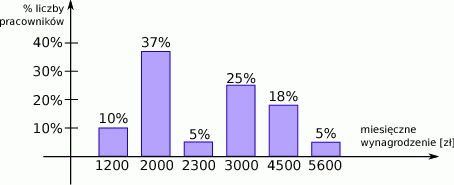
Podaj medianę tych zarobków
Wyznacz średnią kwotę miesięcznych zarobków w tej ﬁrmie.
Oblicz prawdopodobieństwo, że losowo wybrany pracownik tej ﬁrmy zarabia miesięcznie więcej niż 3000 zł.

Zadanie 11

Oblicz z dokładnością do 0,1 odchylenie standardowe następujących danych:

-2; 0; 1; 4; 7; 14.
Wartość -3 -1 0 4 6
Liczebność 10 6 4 2 3

Zadanie 12

Uczeń otrzymał pięć ocen: 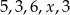5 ,3,6,x,3 . Średnia arytmetyczna tych ocen jest równa 4. Oblicz i medianę tych pięciu ocen.

Zadanie 13

Wyniki klasówki z matematyki, której średnia ocen była równa 3,5 przedstawiono w tabeli.

Oceny	1	2	3	4	5	6
Liczba uczniów	2	2		9	3	2

Oblicz .
Oblicz medianę danych.

Zadanie 14

Tabela przedstawia wyniki uzyskane na sprawdzianie przez uczniów klasy III.

Oceny	6	5	4	3	2	1
Liczba uczniów	1	2	6	5	9	2

Oblicz średnią arytmetyczną i kwadrat odchylenia standardowego uzyskanych ocen.

Zadanie 15

Tabela zawiera niektóre wyniki pisemnego sprawdzianu z matematyki w pewnej klasie maturalnej (ocenionego w sześciostopniowej skali ocen).

	Dziewczęta	Chłopcy
liczba osób	11	14
średnia ocen	4,0	3,8
odchylenie standardowe	1,1	1,8

Oblicz średnią ocen z tego sprawdzianu oraz odchylenie standardowe dla całej klasy. Wyniki podaj z zaokrągleniem do jednego miejsca po przecinku.

Zadanie 16

Średnia wieku 15 mieszkańców pewnego bloku wynosi 33 lata. Gdy do wolnego mieszkania wprowadził się nowy mieszkaniec, średnia zwiększyła się o 1 rok. Ile lat ma nowy mieszkaniec?

Zadanie 17

Oblicz medianę danych: 0, 1, 3, 3, 1, 1, 2, 1.

Zadanie 18

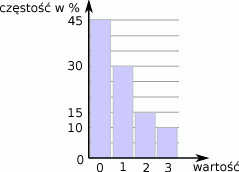
Oblicz średnią arytmetyczną danych przedstawionych na poniższym diagramie częstości

Zadanie 19

Marek waha się, który obóz letni wybrać. Aby podjąć najlepszą decyzję sporządził tabelkę i obliczył średnie ważone. Który obóz powinien wybrać?

	Koszt (waga 0,4)	Termin (waga 0,1)	Towarzystwo (waga 0,3)	Atrakcyjność (waga 0,2)	Średnia
Obóz wędkarski	8	2	8	4
Obóz żeglarski	4	4	6	7
Obóz rowerowy	7	6	5	5

Zadanie 20

Tabela przedstawia wyniki części teoretycznej egzaminu na prawo jazdy. Zdający uzyskał wynik pozytywny, jeżeli popełnił co najwyżej dwa błędy.

Liczba błędów	0	1	2	3	4	5	6	7	8
Liczba zdających	8	5	8	5	2	1	0	0	1

Oblicz średnią arytmetyczną liczby błędów popełnionych przez zdających ten egzamin. Wynik podaj w zaokrągleniu do całości.
Oblicz prawdopodobieństwo, że wśród dwóch losowo wybranych zdających tylko jeden uzyskał wynik pozytywny. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.

Zadanie 21

Tabela przedstawia dane dotyczące wieku kobiet i mężczyzn pracujących w małej ﬁrmie zatrudniającej 7 osób:

	Kobiety	Mężczyźni
Liczba osób	3	4
Średni wiek	26	33
Odchylenie standardowe	1,4	4,6

Wyznacz średnie odchylenie standardowe liczone dla wszystkich osób pracujących w tej ﬁrmie.

Zadanie 22

Mediana trzech liczb jest równa 4, a ich średnia arytmetyczna jest równa 5. Oblicz sumę największej i najmniejszej z tych liczb.

Zadanie 23

Pewna maszyna wykonuje śruby o średnicy 14 mm. Dokonano kontroli jakości wykonywanych śrub i jej wyniki zebrano w tabeli.

Średnica w mm	13,8	13,9	14	14,1	14,2
Liczba śrub	8	17	48	13	14

Opierając się na podanych danych.

Oblicz średnią średnicę śruby.
Oblicz prawdopodobieństwo wyprodukowania śruby o średnicy z przedziału .
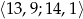Oblicz odchylenie standardowe średnicy śruby. Wynik podaj z dokładnością do 0,01.

Zadanie 24

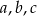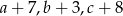Średnia arytmetyczna liczb a,b,c jest równa 15. Oblicz średnią arytmetyczną liczb a+ 7 ,b+ 3 ,c+ 8 .

Zadanie 25

Sprzedawca kwiatów notował w tabeli ilość otrzymanych banknotów z podziałem według ich nominałów.

	1 dzień	2 dzień	3 dzień	4 dzień	5 dzień
10 zł	2	7	4	6	1
20 zł	5	5	2	4	3
50 zł	2	3	0	3	5
100 zł	1	3	1	1	2

Podaj, w których dniach jego przychody były wyższe niż średni dzienny przychód w ciągu tych pięciu dni.
Oblicz odchylenie standardowe liczby otrzymanych banknotów w ciągu tych pięciu dni. Wynik podaj z dokładnością do 0,1.

Zadanie 26

Oblicz medianę następujących danych: 13,2; 15; 12,225; 14; 16,8; 42,7; 22,1; 31,4; 20,6; 18,4.

Zadanie 27

Oblicz medianę danych przedstawionych w postaci tabeli liczebności

Wartość	0	1	2	3
Liczebność	4	3	1	1

Zadanie 28

Na poniższym diagramie przedstawiono zbiorcze wyniki z egzaminu maturalnego z matematyki na poziomie rozszerzonym w 2008 roku. Diagram przedstawia rozkład wyników pogrupowanych w zależności od procentowego wyniku egzaminu.

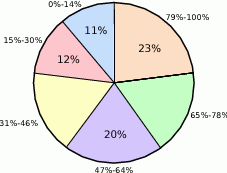
Wiedząc, że egzamin na poziomie rozszerzonym zdawało 40598 maturzystów oblicz, ilu maturzystów uzyskało wynik w przedziale 0%–30%.
Wiedząc, że 60% maturzystów uzyskało z egzaminu co najmniej 47% punktów oblicz, jaki procent maturzystów uzyskał wynik w przedziale 31%–46%.
Oblicz jakie jest prawdopodobieństwo, że losowo wybrany maturzysta uzyskał wynik poniżej 47%.

Zadanie 29

Na pewnym przejściu granicznym celnicy odprawiają codziennie 200 samochodów ciężarowych. Na wykresie pokazano liczby ciężarówek oczekujących na odprawę celną o godzinie 24.00 każdego z pierwszych ośmiu dni lutego.

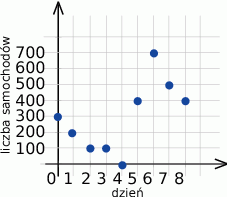
Wymień te dni, w których stanęło w kolejce do odprawy celnej co najmniej 200 samochodów ciężarowych.
Pewnego dnia o północy związkowcy z Samoobrony zablokowali na 24 godziny dojazd do przejścia granicznego. Kiedy to było?
Dziedziną funkcji 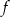jest zbiór 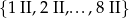. Funkcja 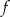każdemu argumentowi przyporządkowuje liczbę ciężarówek, które w danym dniu stanęły w kolejce do odprawy celnej. Podaj wartości tej funkcji.

Arkusz Wersja PDF