Zestaw użytkownika nr 8919_9002
Zestaw użytkownika
nr 8919_9002
Końcami odcinka są punkty o współrzędnych 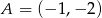 oraz
oraz 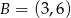 . Odcinek
. Odcinek 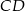 jest obrazem odcinka
jest obrazem odcinka 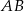 zarówno w jednokładności o dodatniej skali i środku
zarówno w jednokładności o dodatniej skali i środku 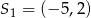 , jak i w jednokładności o ujemnej skali i środku
, jak i w jednokładności o ujemnej skali i środku 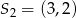 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 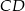 oraz skalę jednokładności o środku
oraz skalę jednokładności o środku 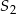 .
.
W trójkącie 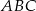 dane są:
dane są: 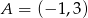 ,
, ![→ AB = [5,− 4]](https://img.zadania.info/zad/4852794/HzadT2x.gif) oraz
oraz ![→ BC = [2,6]](https://img.zadania.info/zad/4852794/HzadT3x.gif) . Trójkąt
. Trójkąt 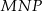 jest obrazem trójkąta
jest obrazem trójkąta 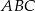 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 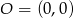 i skali
i skali 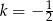 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 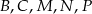 .
.
Punkty 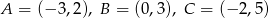 to wierzchołki trójkąta. Podaj, jakie są współrzędne wierzchołków trójkąta symetrycznego do trójkąta
to wierzchołki trójkąta. Podaj, jakie są współrzędne wierzchołków trójkąta symetrycznego do trójkąta 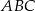 względem
względem
- osi
 ,
, - osi
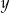 ,
, - punktu
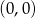 .
.
Na paraboli o równaniu 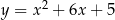 znajdź współrzędne punktu
znajdź współrzędne punktu 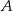 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 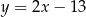 jest najmniejsza.
jest najmniejsza.
Na prostej 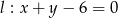 wyznacz taki punkt
wyznacz taki punkt 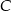 , aby długość łamanej
, aby długość łamanej 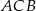 , gdzie
, gdzie 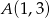 ,
, 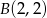 , była najmniejsza. Uzasadnij swoje rozumowanie.
, była najmniejsza. Uzasadnij swoje rozumowanie.
Dane są punkty 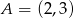 i
i 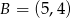 . Na prostej o równaniu
. Na prostej o równaniu 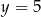 wyznacz punkt
wyznacz punkt 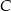 tak, aby łamana
tak, aby łamana 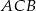 miała jak najmniejszą długość. Odpowiedź uzasadnij.
miała jak najmniejszą długość. Odpowiedź uzasadnij.
Dane są punkty 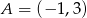 i
i 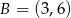 . Funkcja
. Funkcja 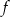 przyporządkowuje dowolnemu punktowi należącemu do odcinka
przyporządkowuje dowolnemu punktowi należącemu do odcinka 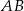 jego odległość od punktu
jego odległość od punktu 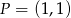 . Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.
. Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.

