Zestaw użytkownika nr 8980_4766

Zestaw użytkownika
nr 8980_4766

Zadanie 1
(5 pkt)

Huta szkła produkuje kulki szklane o promieniu 5 cm. Do wysyłki będą one pakowane po 4 sztuki w sztywne pudełka w kształcie walca, którego wysokość wynosi 10 cm, a średnica 24 cm. Czy dobrze została dobrana średnica tych pudełek?

Zadanie 2
(5 pkt)

Przyprostokątne trójkąta 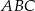ABC mają długości 10 i 24. Przeciwprostokątna trójkąta 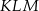KLM podobnego do niego ma długość 39. Oblicz pole trójkąta KLM .

Zadanie 3
(5 pkt)

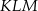Drużyna żeglarska, płynąc po największym polskim jeziorze Śniardwy, odległość między dwiema przystaniami, która na mapie w skali 1:1 000 000 wynosi 5 cm, pokonała w czasie 2 godzin i 30 min. Oblicz średnią prędkość żaglówki.

Zadanie 4
(5 pkt)

Uprość wyrażenie 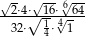√2⋅4⋅√-16⋅6√-64 32⋅√ 1⋅√41 4 .

Zadanie 5
(5 pkt)

Cena pewnego towaru wraz z 7% podatkiem VAT wynosi 69,55zł. Ile będzie kosztował ten sam towar jeżeli podatek VAT zostanie zwiększony do 22%?

Zadanie 6
(5 pkt)

Wnuczek ma tyle miesięcy co dziadek lat. Razem maja 91 lat. Ile lat ma dziadek, a ile wnuczek?

Zadanie 7
(5 pkt)

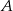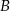Na zlecenie klienta makler ma kupić akcje spółek A i B za 1000 zł. Cena jednej akcji spółki 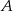A jest równa 4,25 zł, a jedna akcja spółki 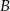B kosztuje 6,75 zł. Ile maksymalnie akcji każdego rodzaju makler może kupić, jeśli tańszych ma być o 10 więcej niż droższych?

Zadanie 8
(5 pkt)

Oblicz objętość i pole powierzchni graniastosłupa, którego podstawą jest romb o przekątnych długości 6 cm i 8 cm, którego przekątna ściany bocznej tworzy z krawędzią podstawy kąt o mierze 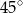45∘ .

Zadanie 9
(5 pkt)

Świeżo skoszona trawa zawiera 60% wody, a wysuszone siano tylko 15% wody. Oblicz, ile kilogramów wysuszonego siana można otrzymać z 1 tony skoszonej trawy? Wynik podaj w zaokrągleniu do pełnych kilogramów.

Zadanie 10
(5 pkt)

Średni wiek w pewnej sześcioosobowej grupie tematycznej na konferencji naukowej wynosił 49 lat. Najmłodszy uczestnik zrezygnował i wówczas średnia wieku wzrosła do 53 lat. Ile lat miał najmłodszy uczestnik?

Zadanie 11
(5 pkt)

W trójkącie równoramiennym wysokość poprowadzona do podstawy ma długość 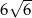√ -- 6 6 . Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.

Zadanie 12
(5 pkt)

Czterej koledzy wybrali się na wakacje nad jezioro odległe o 80 km od miejsca zamieszkania. Po przyjeździe najmłodszy z nich zobaczył, że na mapie w skali 1:400 000 powierzchnia jeziora wynosi 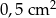0,5 cm 2 . Oblicz rzeczywistą powierzchnię tego jeziora.

Zadanie 13
(5 pkt)

Jaka jest wysokość budynku rzucającego cień długości 19 m w momencie, gdy promienie słoneczne padają pod kątem 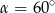α = 60∘ . Wynik podaj z dokładnością do 10 cm.

Zadanie 14
(5 pkt)

Metalową kulę o promieniu 10 cm i stożek o średnicy 16 cm i wysokości 12cm przetopiono. Następnie z otrzymanego metalu wykonano walec o średnicy 8cm. Jaką wysokość ma ten walec?

Zadanie 15
(5 pkt)

Z okrągłego obrusa o średnicy 2 m mama Jadzi chce zrobić kwadratowy obrus o boku 140 cm. Czy to będzie możliwe, jeśli kwadratowy obrus ma być z jednego kawałka materiału?

Zadanie 16
(5 pkt)

Asi zerwał się naszyjnik. Trzecią część korali znalazła na podłodze, jedna czwarta w kieszeni, jedna piąta pod oparciem kanapy, a szósta część korali została na sznurku. Sześciu korali nie udało się jej odnaleźć. Oblicz, ile korali zostało na sznurku?

Zadanie 17
(5 pkt)

W dwóch naczyniach jest woda. Gdyby z pierwszego naczynia przelano do drugiego 2 litry wody, to w obu naczyniach byłoby jej tyle samo. Gdyby zaś z drugiego do pierwszego przelano 3 litry wody, to w pierwszym naczyniu byłoby jej sześć razy więcej niż w drugim. Ile jest wody w obu naczyniach?

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze