Zestaw użytkownika nr 8982_4089
Zestaw użytkownika
nr 8982_4089
Podstawą graniastosłupa jest trójkąt prostokątny równoramienny o ramieniu długości 9. Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 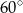 . Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
. Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
W kulę o promieniu długości 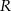 wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
Pole powierzchni bocznej stożka jest cztery razy większe od pola podstawy. Obwód przekroju osiowego stożka jest równy 30. Oblicz objętość tego stożka
Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość  .
.
W ostrosłupie prawidłowym trójkątnym kąt płaski przy wierzchołku ostrosłupa ma miarę  , zaś odległość wierzchołka podstawy od krawędzi bocznej, do której nie należy, jest równa
, zaś odległość wierzchołka podstawy od krawędzi bocznej, do której nie należy, jest równa 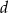 . Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
W pojemniku o kształcie walca o promieniu podstawy 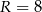 umieszczono dwie kule o promieniu
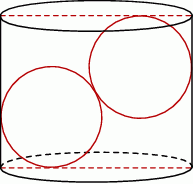
umieszczono dwie kule o promieniu  , w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.
, w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.
Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 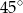 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
Podstawą ostrosłupa jest trójkąt prostokątny, którego kąt ostry ma miarę 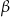 . Wszystkie krawędzie boczne mają długość
. Wszystkie krawędzie boczne mają długość 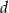 i są nachylone do płaszczyzny podstawy pod kątem o mierze
i są nachylone do płaszczyzny podstawy pod kątem o mierze  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość 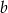 , a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę
, a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest półkolem. Oblicz miarę kąta rozwarcia stożka.
Punkty 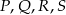 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 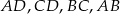 czworościanu
czworościanu 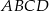 . Wykaż, że punkty
. Wykaż, że punkty 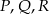 i
i 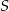 są wierzchołkami równoległoboku.
są wierzchołkami równoległoboku.
Odległość środka wysokości ostrosłupa prawidłowego trójkątnego od ściany bocznej jest równa 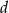 . Krawędź boczna tworzy z płaszczyzną podstawy kąt
. Krawędź boczna tworzy z płaszczyzną podstawy kąt  . Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
Do sześciennego pudła o boku długości 60 cm, włożono walec, który jest styczny do przylegających ścian. Jak dużą kulkę można jeszcze zmieścić w wolnym rogu pudła?
Wszystkie krawędzie boczne ostrosłupa trójkątnego 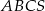 o wierzchołku
o wierzchołku 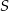 mają długość
mają długość 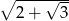 . Wiedząc, że
. Wiedząc, że 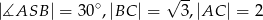 oblicz objętość tego ostrosłupa.
oblicz objętość tego ostrosłupa.
Przekrój stożka wyznaczony przez wierzchołek i cięciwę podstawy jest trójkątem równobocznym, o polu równym 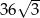 . Płaszczyzna
. Płaszczyzna  , do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej
, do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej 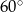 . Oblicz objętość stożka.
. Oblicz objętość stożka.
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym wysokość ma długość 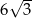 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt  taki, że
taki, że 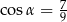 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Pole powierzchni całkowitej 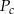 stożka oraz jego pole podstawy
stożka oraz jego pole podstawy 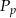 spełniają równanie
spełniają równanie 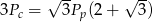 . Oblicz miarę kąta rozwarcia stożka.
. Oblicz miarę kąta rozwarcia stożka.

