Zestaw użytkownika nr 8989_1120
Zestaw użytkownika
nr 8989_1120
Ciąg 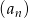 , gdzie
, gdzie 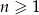 , jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji
, jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji 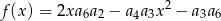 .
.
Ciąg 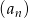 dany jest wzorem
dany jest wzorem 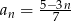 , dla
, dla 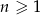 .
.
- Oblicz sumę
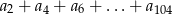 .
. - Ustalmy
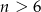 . Dla jakich
. Dla jakich  liczby
liczby 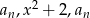 są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 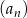 dla każdego
dla każdego 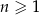 określona jest wzorem
określona jest wzorem 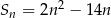 .
.
- Wykaż, że ciąg
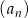 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Wykaż, że jeżeli suma
 początkowych wyrazów ciągu dla każdego
początkowych wyrazów ciągu dla każdego 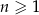 określona jest wzorem
określona jest wzorem 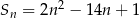 , to ciąg ten nie jest arytmetyczny.
, to ciąg ten nie jest arytmetyczny. - Znajdź takie trzy kolejne wyrazy ciągu
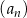 , aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
, aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
Wyrazy 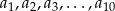 pewnego nieskończonego ciągu
pewnego nieskończonego ciągu 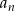 spełniają warunki
spełniają warunki 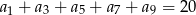 ,
, 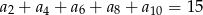 . Wiedząc, że nieskończony ciąg
. Wiedząc, że nieskończony ciąg 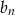 określony wzorem
określony wzorem 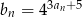 jest ciągiem geometrycznym, oblicz sumę wszystkich wyrazów ciągu
jest ciągiem geometrycznym, oblicz sumę wszystkich wyrazów ciągu 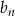 .
.
W trójkącie prostokątnym długości wysokości i środkowej poprowadzonej z wierzchołka kąta prostego oraz długość przeciwprostokątnej tworzą ciąg geometryczny, w którym iloczyn wyrazów jest równy 8. Oblicz promień okręgu wpisanego w ten trójkąt.
W kąt o mierze  wpisano ciąg kół w taki sposób, że pierwsze koło ma promień
wpisano ciąg kół w taki sposób, że pierwsze koło ma promień  i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.
i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.

