Zestaw użytkownika nr 8997_1307
Zestaw użytkownika
nr 8997_1307
Rozwiąż nierówność 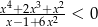 .
.
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 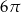 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 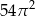 B)
B) 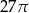 C)
C) 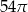 D)
D) 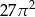
Oceń, czy liczba 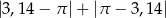 jest wymierna, czy niewymierna.
jest wymierna, czy niewymierna.
Miara kąta  jest równa:
jest równa:
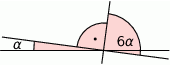
A) 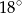 B)
B) 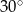 C)
C) 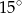 D)
D) 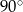
Okrąg o równaniu 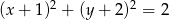 :
:
A) nie przecina osi 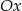 ,
,
B) nie przecina osi 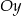 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 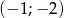 .
.
W ciągu arytmetycznym 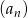 pierwszy wyraz jest równy
pierwszy wyraz jest równy 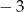 , zaś
, zaś 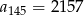 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba
A) 13 B) 14 C) 15 D) 16
Znajdź wszystkie liczby całkowite spełniające nierówność 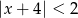 .
.
Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 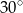 . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
. Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
Podaj wzór na wyraz ogólny ciągu 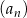 określonego w następujący sposób: ciąg
określonego w następujący sposób: ciąg 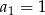 jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
Stosunek miar kątów czworokąta jest równy 1:2:3:4. Zatem najmniejszy kąt tego wielokąta ma miarę
A) 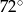 B)
B) 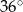 C)
C) 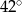 D)
D) 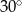
Pan Adam wpłacił na rachunek w funduszu inwestycyjnym pewną kwotę pieniędzy. Po roku stan rachunku zwiększył się o 4,5%, w drugim roku zmniejszył się o 5%, a w trzecim roku wzrósł o 4%. Wiedząc, że stan rachunku pana Adama po trzech latach oszczędzania wynosi 1548,69 zł oblicz jaką kwotę pan Adam początkowo wpłacił na ten rachunek.
Wskaż 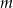 , dla którego funkcja liniowa
, dla którego funkcja liniowa 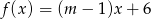 jest rosnąca
jest rosnąca
A) 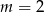 B)
B) 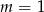 C)
C) 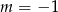 D)
D) 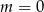
Promień okręgu o równaniu 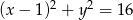 jest równy
jest równy
A) 1 B) 2 C) 4 D) 3
Obwód czworokąta wypukłego 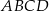 jest równy 50 cm. Obwód trójkąta
jest równy 50 cm. Obwód trójkąta 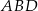 jest równy 46 cm, a obwód trójkąta
jest równy 46 cm, a obwód trójkąta 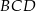 jest równy 36 cm. Oblicz długość przekątnej
jest równy 36 cm. Oblicz długość przekątnej 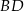 .
.
Na rysunku jest przedstawiony wykres funkcji 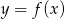 .
.
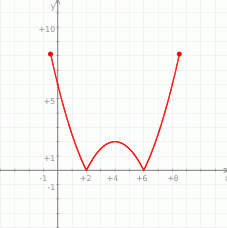
Które równanie ma dokładnie trzy rozwiązania?
A) 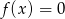 B)
B) 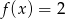 C)
C) 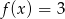 D)
D) 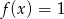
Odwrotność liczby będącej rozwiązaniem równania 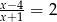 jest równa
jest równa
A) 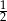 B) 6 C)
B) 6 C) 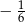 D)
D) 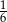
Dane są funkcje 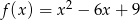 i
i 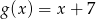 .
.
- Znajdź te argumenty, dla których zarówno funkcja
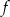 , jak i funkcja
, jak i funkcja 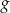 przyjmują wartości dodatnie.
przyjmują wartości dodatnie. - Uzasadnij, że dla każdej liczby całkowitej
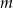 liczba
liczba 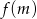 jest kwadratem liczby całkowitej. Kwadratem jakiej liczby naturalnej jest
jest kwadratem liczby całkowitej. Kwadratem jakiej liczby naturalnej jest 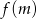 , jeżeli
, jeżeli 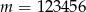 ?
?
Funkcja 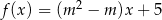 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 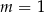 B)
B) 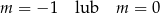 C)
C) 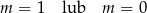 D)
D) 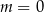
Cenę nart obniżono latem o 20%, a potem jeszcze o 15%. Po tych dwóch obniżkach narty kosztowały 705 zł i 50 gr. Wynika z tego, że pierwotna cena nart to
A) 1100 zł B) 1037,5 zł C) 980 zł D) 952,42 zł
Liczba wszystkich krawędzi graniastosłupa jest równa 24. Wówczas podstawą tego graniastosłupa jest:
A) ośmiokąt B) dwunastokąt C) dziesięciokąt D) sześciokąt
Liczby 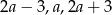 , w podanej kolejności, tworzą ciąg geometryczny. Wyznacz
, w podanej kolejności, tworzą ciąg geometryczny. Wyznacz  .
.
Rozwiąż układ równań:
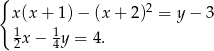
Ewa jadąc drogą widziała elektrownię wiatrową oznaczoną na rysunku literą 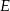 . Z punktu
. Z punktu 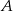 widziała ją pod kątem
widziała ją pod kątem 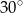 stopni do kierunku drogi. A z punktu
stopni do kierunku drogi. A z punktu 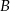 pod kątem
pod kątem 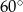 . Przejeżdżając przez punkt
. Przejeżdżając przez punkt 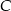 minęła elektrownię. Długość odcinka
minęła elektrownię. Długość odcinka 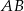 jest równa 20km.
jest równa 20km.
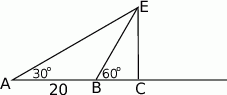
- Oblicz miary kątów
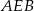 i
i 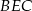 .
. - Oblicz długość odcinka
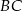 .
. - Oblicz odległość elektrowni od drogi.
W rachunkach przyjmij, że 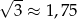 .
.
Romb o kącie ostrym 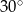 jest opisany na okręgu o promieniu 2. Oblicz pole tego rombu.
jest opisany na okręgu o promieniu 2. Oblicz pole tego rombu.
Suma dwóch liczb równa jest 6. Znajdź te liczby, jeśli wiadomo, że suma podwojonego kwadratu jednej z nich i kwadratu drugiej jest najmniejsza z możliwych.
Ze zbioru liczb 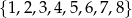 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 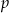 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 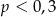 B)
B) 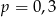 C)
C) 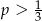 D)
D) 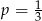
Liczba 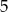 nie należy do dziedziny wyrażenia
nie należy do dziedziny wyrażenia
A) 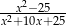 B)
B) 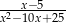 C)
C) 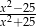 D)
D) 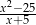
Dla 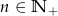 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba
A)  B)
B) 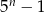 C)
C) 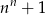 D)
D)