Zestaw użytkownika nr 9004_9386
Zestaw użytkownika
nr 9004_9386
Wykaż, że liczba 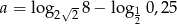 jest liczbą wymierną.
jest liczbą wymierną.
Oblicz 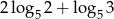 .
.
Uzasadnij, że liczba 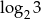 jest niewymierna.
jest niewymierna.
Oblicz wartość wyrażenia 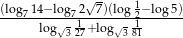 .
.
Wiedząc, że 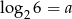 , wyznacz
, wyznacz 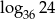 .
.
Oblicz 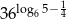 .
.
Nie korzystając z kalkulatora uzasadnij, że: 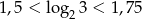 .
.
Udowodnij, że jeśli liczby dodatnie  i
i 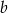 spełniają warunek
spełniają warunek 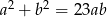 , to
, to 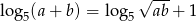 .
.
Wykaż, że liczba 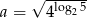 jest liczbą całkowitą.
jest liczbą całkowitą.
Oblicz 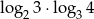 .
.
Uporządkuj rosnąco liczby 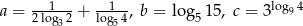 .
.
Wykaż, że 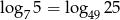 .
.
Widząc, że 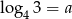 i
i 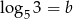 , wyznacz
, wyznacz 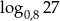 w zależności od
w zależności od  i
i 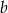 .
.
O liczbach  i
i 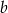 wiadomo, że
wiadomo, że 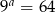 oraz
oraz 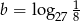 . Oblicz
. Oblicz 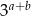 .
.
Uporządkuj rosnąco trzy liczby: 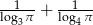 ,
, 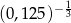 ,
, 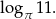 .
.
Liczby dodatnie 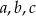 spełniają warunek:
spełniają warunek: 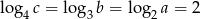 . Oblicz
. Oblicz 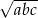 .
.
Oblicz 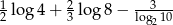 .
.
Wiadomo, że 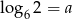 . Wyznacz
. Wyznacz 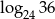 w zależności od
w zależności od  .
.
Oblicz 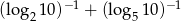 .
.
Wiedząc, że 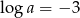 , a
, a 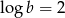 oblicz wartość wyrażenia
oblicz wartość wyrażenia 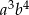 .
.
Wiedząc, że 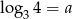 i
i 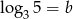 , wyznacz
, wyznacz 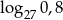 w zależności od
w zależności od  i
i 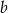 .
.
Udowodnij, że liczby 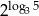 i
i 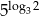 są równe.
są równe.
Wiedząc, że 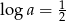 i
i 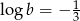 , oblicz
, oblicz 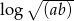 .
.
Wiadomo, że 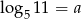 . Wykaż, że
. Wykaż, że 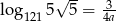 .
.

