Zestaw użytkownika nr 9034_5415
Czas pracy: 45 min.
Na rysunku przedstawiony jest wykres funkcji liniowej  .
.
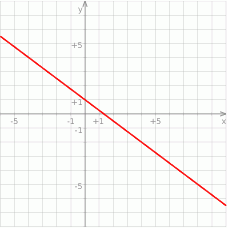
Funkcja 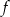 jest określona wzorem
jest określona wzorem
A) 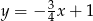 B)
B) 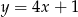 C)
C) 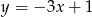 D)
D) 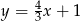
Napisz wzór funkcji liniowej o współczynniku kierunkowym 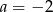 , której wykres przecina oś
, której wykres przecina oś 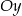 w punkcie
w punkcie 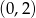 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
Prosta 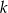 ma równanie
ma równanie 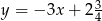 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 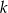 , przechodzącej przez punkt
, przechodzącej przez punkt 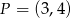 .
.
A) 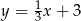 B)
B) 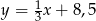 C)
C) 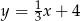 D)
D) 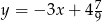
Funkcje 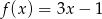 i
i 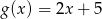 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 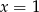 B)
B) 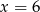 C)
C) 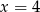 D)
D) 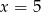
Wyznacz wzór funkcji liniowej, której wykres tworzy z osią 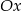 kąt
kąt 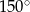 i przechodzi przez punkt
i przechodzi przez punkt 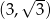 .
.
Dana jest funkcja liniowa 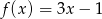 .
.
- Rozwiąż nierówność
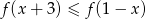 .
. - Podaj maksymalne przedziały monotoniczności funkcji
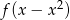 .
.
Wyznacz miejsca zerowe funkcji
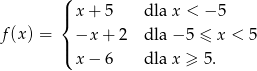
Wiedząc, że zbiorem wartości funkcji 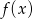 jest przedział
jest przedział 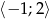 wyznacz wszystkie wartości
wyznacz wszystkie wartości 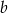 , dla których funkcja
, dla których funkcja 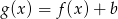 nie ma miejsc zerowych.
nie ma miejsc zerowych.
Dla jakich wartości parametru 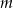 funkcja
funkcja 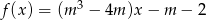 jest:
jest:
- malejąca
- nieparzysta
- parzysta
Liczba  jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 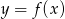 . Wyznacz miejsca zerowe funkcji:
. Wyznacz miejsca zerowe funkcji: 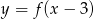 .
.
Oblicz miejsca zerowe funkcji
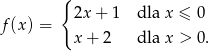
Znajdź wszystkie funkcje liniowe określone na zbiorze 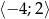 , których zbiorem wartości jest przedział
, których zbiorem wartości jest przedział 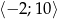 .
.
Wyznacz wzór funkcji liniowej 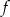 wiedząc, że zbiorem rozwiązań nierówności
wiedząc, że zbiorem rozwiązań nierówności 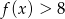 jest przedział
jest przedział 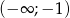 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 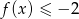 jest przedział
jest przedział 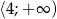 .
.
Funkcja 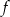 jest określona wzorem
jest określona wzorem
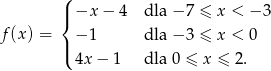
- Podaj dziedzinę funkcji
 .
. - Podaj jej miejsca zerowe.
- Naszkicuj wykres tej funkcji.
- Podaj zbiór wartości funkcji
 .
.
Z trzech prostopadłościennych belek 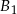 ,
, 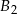 ,
, 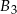 o takich samych przekrojach poprzecznych i długościach odpowiednio równych 1m, 2m, 1m sklejono jedną belkę o długości 4m. Każda z belek
o takich samych przekrojach poprzecznych i długościach odpowiednio równych 1m, 2m, 1m sklejono jedną belkę o długości 4m. Każda z belek 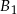 ,
, 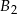 ,
,  wykonana jest z innego materiału, a ich masy są równe odpowiednio 20kg, 30kg, 10kg.
wykonana jest z innego materiału, a ich masy są równe odpowiednio 20kg, 30kg, 10kg.
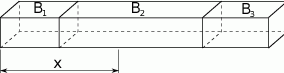
Masa odcinka belki o długosci  jest funkcją zmiennej
jest funkcją zmiennej  . Znajdź wzór tej funkcji.
. Znajdź wzór tej funkcji.
Funkcja liniowa 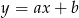 jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal znak wyrażenia
jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal znak wyrażenia 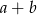 .
.
Funkcja liniowa 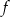 określona jest wzorem
określona jest wzorem 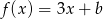 , dla
, dla 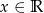 . Wyznacz współczynnik
. Wyznacz współczynnik 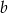 , wiedząc, że
, wiedząc, że 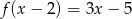 .
.
Wyznacz wzór funkcji liniowej 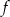 , wiedząc że nie przyjmuje ona wartości dodatnich oraz
, wiedząc że nie przyjmuje ona wartości dodatnich oraz 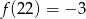 .
.
Wyznacz wzór funkcji liniowej 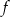 , która dla każdego
, która dla każdego 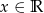 spełnia warunek
spełnia warunek 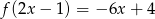 .
.
Wyznacz miejsca zerowe funkcji
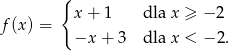
Znajdź wszystkie funkcje liniowe określone na zbiorze 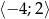 , których zbiorem wartości jest przedział
, których zbiorem wartości jest przedział 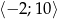 .
.
Wyznacz wzór funkcji liniowej 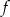 wiedząc, że zbiorem rozwiązań nierówności
wiedząc, że zbiorem rozwiązań nierówności 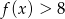 jest przedział
jest przedział 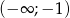 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 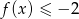 jest przedział
jest przedział 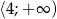 .
.
Wiadomo, że funkcja liniowa 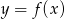 przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy
przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy 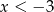 . Ponadto,
. Ponadto, 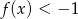 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 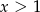 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 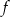 .
.
Funkcja liniowa 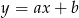 jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal znak wyrażenia
jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal znak wyrażenia 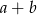 .
.
Zależność między temperaturą wyrażoną w stopniach Fahrenheita, a wyrażoną w stopniach Celsjusza jest zależnością liniową.
- Znajdź tę zależność wiedząc ze
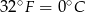 , a
, a 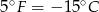 .
. - 22 lipca w San Diego temperatura o godzinie
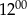 była o
była o 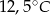 wyższa niż temperatura o godzinie
wyższa niż temperatura o godzinie 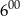 . Wyraź wzrost temperatury w stopniach Fahrenheita.
. Wyraź wzrost temperatury w stopniach Fahrenheita.

