Zestaw użytkownika nr 9082_5029
funkcja20 Kwietnia 2012Czas pracy: 20 min.Suma punktów: 23
Zadanie 1
(1 pkt)
Dziedziną funkcji 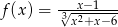 jest zbiór
jest zbiór
A) 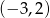 B)
B) 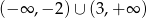 C)
C) 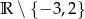 D)
D) 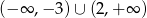
Zadanie 2
(5 pkt)
Na rysunku przedstawiony jest wykres funkcji 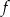 określonej wzorem
określonej wzorem 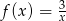 dla
dla 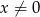 .
.
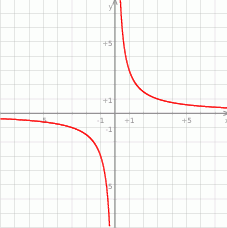
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 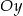 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 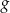 o wzorze
o wzorze 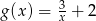 dla
dla 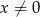 .
.
- Narysuj wykres funkcji
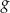 .
. - Oblicz największą wartość funkcji
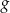 w przedziale
w przedziale 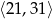 .
. - Podaj, o ile jednostek wzdłuż osi
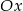 należy przesunąć wykres funkcji
należy przesunąć wykres funkcji 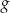 , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
Zadanie 3
(5 pkt)
Dana jest funkcja 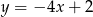 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor
. Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor ![→ v = [2,0]](https://img.zadania.info/zad/9122741/HzadT1x.gif) . Narysuj oba wykresy.
. Narysuj oba wykresy.
Zadanie 4
(5 pkt)
Napisz wzór funkcji liniowej o współczynniku kierunkowym 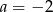 , której wykres przecina oś
, której wykres przecina oś 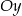 w punkcie
w punkcie 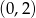 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
Zadanie 5
(1 pkt)
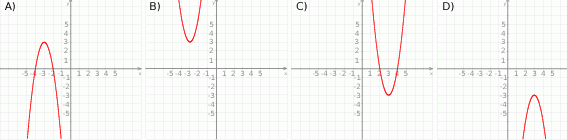
Zbiór wartości funkcji kwadratowej 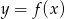 jest rozłączny z przedziałem
jest rozłączny z przedziałem 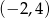 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 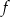 ?
?
Zadanie 6
(1 pkt)
Funkcja 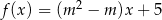 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 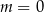 B)
B) 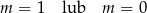 C)
C) 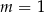 D)
D) 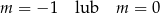
Zadanie 7
(5 pkt)
Dany jest wykres funkcji logarytmicznej 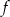 .
.
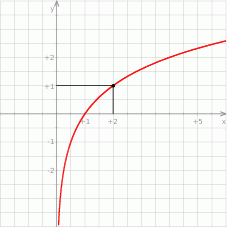
- Wyznacz wzór funkcji
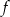 .
. - Narysuj wykres funkcji
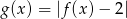 .
. - Odczytaj z rysunku zbiór argumentów, dla których wartości funkcji
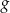 są nie mniejsze od wartości funkcji
są nie mniejsze od wartości funkcji 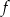 .
.

