Zestaw użytkownika nr 9115_5140
Zestaw użytkownika
nr 9115_5140
Wyznacz najmniejszą i największą wartość funkcji 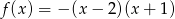 w przedziale
w przedziale 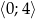 .
.
Wyznacz wzór funkcji 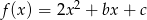 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 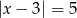 .
.
Określ zbiór wartości funkcji: 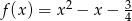 . Dla jakich argumentów funkcja przyjmuje wartości ujemne?
. Dla jakich argumentów funkcja przyjmuje wartości ujemne?
Funkcja kwadratowa 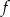 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu -4, a do jej wykresu należy punkt
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu -4, a do jej wykresu należy punkt 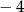 . Napisz wzór funkcji
. Napisz wzór funkcji 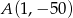 w postaci ogólnej.
w postaci ogólnej.
Jedynym miejscem zerowym funkcji kwadratowej 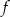 jest liczba 2. Wykres funkcji
jest liczba 2. Wykres funkcji 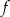 przecina oś
przecina oś 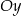 w punkcie o współrzędnych
w punkcie o współrzędnych 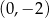 . Wyznacz wzór tej funkcji w postaci ogólnej.
. Wyznacz wzór tej funkcji w postaci ogólnej.
Funkcja kwadratowa 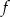 określona jest wzorem
określona jest wzorem 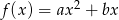 . Wiadomo, że
. Wiadomo, że 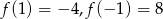 . Określ, dla jakich argumentów spełniona jest nierówność
. Określ, dla jakich argumentów spełniona jest nierówność 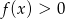 .
.
Wyznacz wartość funkcji 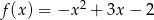 dla argumentu
dla argumentu 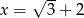 .
.
Funkcja 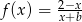 przyjmuje wartości ujemne wtedy i tylko wtedy gdy
przyjmuje wartości ujemne wtedy i tylko wtedy gdy 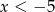 lub
lub 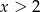 .
.
- Oblicz
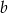 .
. - Napisz wzór funkcji
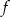 w postaci kanonicznej.
w postaci kanonicznej. - Wyznacz zbiór tych argumentów, dla których funkcja
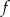 osiąga wartości nie większe niż funkcja
osiąga wartości nie większe niż funkcja 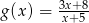 .
.

