Zestaw użytkownika nr 9250_6638
Zestaw użytkownika
nr 9250_6638
Napisz wzór funkcji liniowej o współczynniku kierunkowym 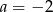 , której wykres przecina oś
, której wykres przecina oś 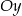 w punkcie
w punkcie 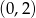 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
Dana jest funkcja 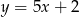 .
.
- Oblicz miejsce zerowe funkcji.
- Podaj współrzędne punktu przecięcia wykresu z osią
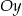 .
. - Oblicz wartość funkcji dla argumentu równego -2.
- Oblicz, dla jakiego argumentu wartość funkcji wynosi -3.
- Czy jest to funkcja rosnąca? Dlaczego?
Dana jest funkcja 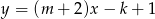 , gdzie
, gdzie  . Dla jakich wartości
. Dla jakich wartości  i
i 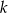 funkcja ta jest stała, a wykres jej jest prostą przecinającą oś
funkcja ta jest stała, a wykres jej jest prostą przecinającą oś 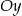 poniżej początku układu współrzędnych?
poniżej początku układu współrzędnych?
Wykaż, że iloczyn trzech kolejnych liczb podzielnych przez 3 dzieli się przez 81.
Wykaż, że liczba 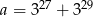 jest podzielna przez 30.
jest podzielna przez 30.
Wykaż, że jeżeli przy dzieleniu przez 7 jedna liczba daję resztę 3, a druga resztę 4, to iloczyn tych liczb daje przy dzieleniu przez 7 resztę 5.
Wyznacz 155-tą cyfrę po przecinku rozwinięcia dziesiętnego liczby 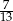 .
.
W pierwszym miesiącu wydawnictwo sprzedawało książkę po cenie 20 zł. W drugim miesiącu cenę obniżono o 10%, co spowodowało wzrost przychodów o 8%. O ile procent więcej książek sprzedano w drugim miesiącu niż w pierwszym?
Świeżo skoszona trawa zawiera 60% wody, a wysuszone siano tylko 15% wody. Oblicz, ile kilogramów wysuszonego siana można otrzymać z 1 tony skoszonej trawy? Wynik podaj w zaokrągleniu do pełnych kilogramów.
Stężenie pewnego roztworu wodnego soli wynosi 5%. Ile kilogramów czystej wody należy dodać do 90 kg tego roztworu, aby otrzymać roztwór o stężeniu 2%?
Za normalne i ulgowe bilety kolejowe zapłacono 3250 zł. Stosunek liczby biletów normalnych do biletów ulgowych był równy 3:2 i jeden bilet ulgowy był o 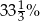 tańszy od biletu normalnego. Oblicz, ile zapłacono za bilety ulgowe.
tańszy od biletu normalnego. Oblicz, ile zapłacono za bilety ulgowe.
Długości obu podstaw trapezu wydłużono o 25%. O ile procent należy skrócić jego wysokość aby pole trapezu nie uległo zmianie?
Podaj miejsca zerowe funkcji 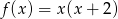 .
.
Zbieramy z Olkiem znaczki i wczoraj Olek mi powiedział, że ma już 155 znaczków angielskich, francuskich i hiszpańskich. Francuskich ma 2 razy więcej niż hiszpańskich, a angielskich o 39 mniej niz francuskich i hiszpańskich razem. To jednak niemożliwe, uzasadnij dlaczego Olek musiał się pomylić.
Średni wiek w pewnej sześcioosobowej grupie tematycznej na konferencji naukowej wynosił 49 lat. Najmłodszy uczestnik zrezygnował i wówczas średnia wieku wzrosła do 53 lat. Ile lat miał najmłodszy uczestnik?
Uzasadnij, że jeżeli  jest dowolną cyfrą, to mnożąc liczbę 37037 przez liczbę
jest dowolną cyfrą, to mnożąc liczbę 37037 przez liczbę 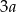 otrzymamy liczbę, której wszystkie cyfry są równe
otrzymamy liczbę, której wszystkie cyfry są równe  .
.
Gdyby Aleksander Wielki umarł o 5 lat wcześniej, to panowałby przez 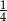 swego życia. Gdyby żył o 9 lat dłużej, to panowałby przez połowę swego życia. Ile lat żył i ile lat panował.
swego życia. Gdyby żył o 9 lat dłużej, to panowałby przez połowę swego życia. Ile lat żył i ile lat panował.
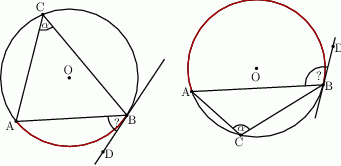
Prosta 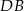 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 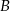 . Oblicz miarę zaznaczonego kąta
. Oblicz miarę zaznaczonego kąta 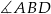 jeśli
jeśli 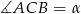 .
.
Liczby 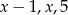 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Oblicz miarę kąta wpisanego opartego na średnicy okręgu.
W trójkącie 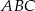 prowadzimy dwusieczną kąta
prowadzimy dwusieczną kąta 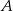 i przez punkt
i przez punkt 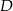 przecięcia się tej dwusiecznej z bokiem
przecięcia się tej dwusiecznej z bokiem 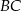 prowadzimy proste równoległe do boków
prowadzimy proste równoległe do boków 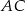 i
i 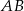 , które przecianją te boki odpowiednio w punktach
, które przecianją te boki odpowiednio w punktach 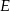 i
i 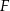 . Wykaż, że czworokąt
. Wykaż, że czworokąt 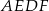 jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
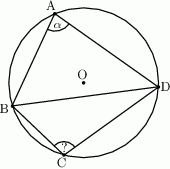
Wszystkie wierzchołki czworokąta 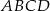 leżą na okręgu oraz
leżą na okręgu oraz 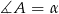 . Oblicz miarę kąta
. Oblicz miarę kąta 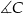 .
.
Obwód trapezu równoramiennego wynosi 32 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 3 cm i 11 cm. Oblicz pole trapezu.
Punkt 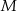 przyprostokątnej
przyprostokątnej 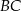 trójkąta prostokątnego
trójkąta prostokątnego 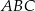 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 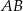 otrzymując punkt
otrzymując punkt 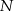 . Wykazać, że
. Wykazać, że 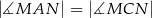 .
.
Z dwóch przeciwległych wierzchołków kwadratu o boku 2 zakreślono okręgi o promieniu 2. Oblicz pole „soczewki” wyznaczonej przez te okręgi.
Trójkąt równoboczny, kwadrat i sześciokąt foremny mają ten sam obwód długości 10cm. Oblicz pole każdej z tych figur. Która z nich ma największe pole, a która najmniejsze?
Wierzchołek 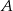 trójkąta ostrokątnego
trójkąta ostrokątnego 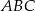 połączono odcinkiem ze środkiem
połączono odcinkiem ze środkiem 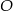 okręgu opisanego. Z wierzchołka
okręgu opisanego. Z wierzchołka 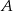 poprowadzono wysokość
poprowadzono wysokość 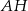 . Wykaż, że
. Wykaż, że 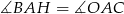 .
.
Udowodnij, że przekątna 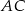 kwadratu
kwadratu 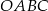 jest równa przekątnej
jest równa przekątnej 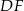 prostokąta
prostokąta 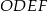 .
.
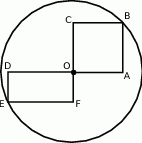
Dwusieczne kątów przyległych do boku 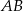 trójkąta
trójkąta 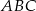 przecinają się w punkcie
przecinają się w punkcie 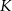 . Odległość punktu
. Odległość punktu 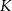 od odcinka
od odcinka 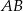 wynosi 3. Jaka jest odległość punktu
wynosi 3. Jaka jest odległość punktu 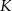 od odcinka
od odcinka 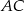 ?
?
Punkt 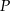 jest punktem przecięcia wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt
jest punktem przecięcia wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt 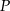 z wierzchołkiem trójkąta ma długość
z wierzchołkiem trójkąta ma długość 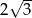 ?
?
Oblicz miary kątów środkowych 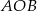 zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego
zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego 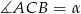 .
.
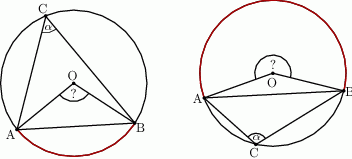
W sześciokącie foremnym połączono środki sąsiednich boków otrzymując ponownie sześciokąt foremny. Oblicz stosunek pól: otrzymanego i wyjściowego sześciokąta.

