Zestaw użytkownika nr 9269_8781
Zestaw użytkownika
nr 9269_8781
Oblicz cosinus kąta jaki tworzą dwie ściany czworościanu foremnego. Podaj przybliżoną miarę tego kąta.
Czworościan foremny przecięto płaszczyzną przechodzącą przez krawędź boczną i wysokość podstawy. Jako przekrój otrzymano trójkąt o polu równym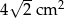 
. Oblicz objętość tego czworościanu.
Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę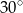 
. Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
Podstawą graniastosłupa prostego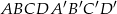 
jest równoległobok 
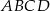o bokach długości 
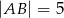i 
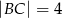. Oblicz długość wysokości 
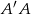graniastosłupa jeżeli 
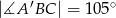oraz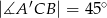 
.
Dany jest graniastosłup prawidłowy czworokątny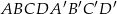 
o podstawach 
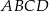i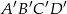 
, oraz krawędziach bocznych 
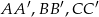i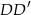 
. Oblicz pole trójkąta 
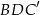wiedząc, że przekątna ściany bocznej ma długość 13 i jest nachylona do podstawy pod takim kątem 
, że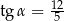 
.
W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez dłuższą przekątną dolnej podstawy oraz przez jedną z krawędzi górnej podstawy. Płaszczyzna ta wyznacza przekrój graniastosłupa, który jest trapezem równoramiennym. Wiedząc, że w trapez ten można wpisać okrąg o promieniu 1, oblicz objętość graniastosłupa.
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym długość wysokości wynosi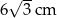 
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze 
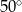. Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1cm.
Podstawą ostrosłupa jest prostokąt o bokach 6cm i 8cm. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod katem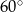 
. Oblicz pole powierzchni ostrosłupa.
Pole powierzchni bocznej stożka jest cztery razy większe od pola podstawy. Obwód przekroju osiowego stożka jest równy 30. Oblicz objętość tego stożka
