Zestaw użytkownika nr 9361_7774
Powtórzenie Funkcja wymierna
Wskaż zbiór, w którym funkcja 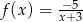 jest rosnąca.
jest rosnąca.
A) 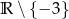 B)
B) 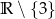 C)
C) 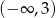 D)
D) 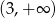
Dana jest funkcja określona wzorem 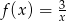 . Wartość tej funkcji w punkcie
. Wartość tej funkcji w punkcie 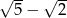 jest równa
jest równa
A) 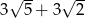 B)
B) 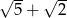 C)
C) 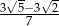 D)
D) 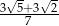
Dziedziną funkcji 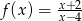 jest zbiór:
jest zbiór:
A) 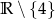 B)
B) 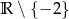 C)
C) 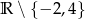 D)
D) 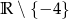
Liczba 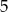 nie należy do dziedziny wyrażenia
nie należy do dziedziny wyrażenia
A) 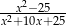 B)
B) 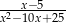 C)
C) 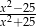 D)
D) 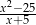
Dziedziną wyrażenia wymiernego 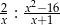 jest zbiór
jest zbiór
A) 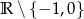 B)
B) 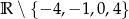 C)
C) 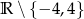 D)
D) 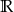
Liczba 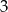 nie należy do dziedziny wyrażenia
nie należy do dziedziny wyrażenia
A) 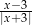 B)
B) 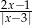 C)
C) 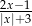 D)
D) 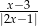
Dziedziną wyrażenia 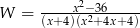 jest zbiór
jest zbiór
A) 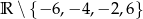 B)
B) 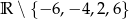 C)
C) 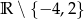 D)
D) 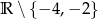
Zbiór 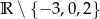 jest dziedziną wyrażenia:
jest dziedziną wyrażenia:
A) 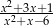 B)
B) 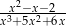 C)
C) 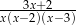 D)
D) 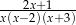
Wykres funkcji 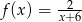 powstaje przez przesunięcie wykresu funkcji
powstaje przez przesunięcie wykresu funkcji 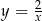 o 6 jednostek
o 6 jednostek
A) w lewo B) w prawo C) w górę D) w dół
Zbiorem wartości funkcji 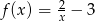 jest
jest
A) 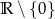 B)
B) 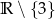 C)
C) 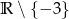 D)
D) 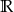
Wykres funkcji 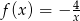 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 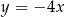 B)
B) 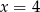 C)
C) 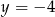 D)
D) 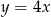
Wykres funkcji 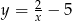 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 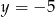 B)
B) 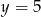 C)
C) 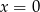 D)
D) 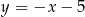
Przedstawiony na rysunku wykres może być wykresem funkcji
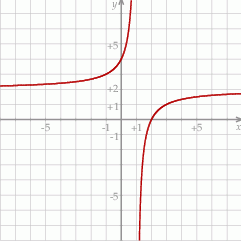
A) 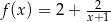 B)
B) 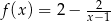 C)
C) 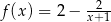 D)
D) 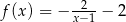
Wykres funkcji 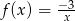 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i IV B) II i III C) I i III D) I i II
Do wykresu funkcji 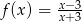 należy punkt
należy punkt
A) 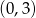 B)
B) 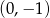 C)
C) 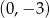 D)
D) 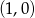
Rozwiąż równanie 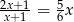 .
.
Rozwiąż równanie 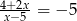 .
.
Rozwiąż nierówność 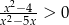 .
.
Na rysunku przedstawiony jest wykres funkcji 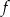 określonej wzorem
określonej wzorem 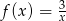 dla
dla 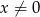 .
.
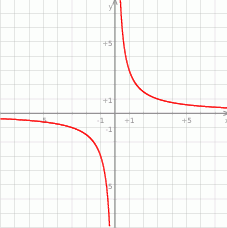
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 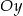 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 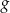 o wzorze
o wzorze 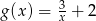 dla
dla 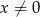 .
.
- Narysuj wykres funkcji
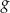 .
. - Oblicz największą wartość funkcji
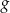 w przedziale
w przedziale 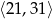 .
. - Podaj, o ile jednostek wzdłuż osi
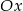 należy przesunąć wykres funkcji
należy przesunąć wykres funkcji 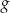 , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
Dane są funkcje 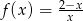 i
i 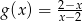 .
.
- Naszkicuj wykresy obu funkcji w jednym układzie współrzędnych.
- Określ przedziały monotoniczności obu funkcji.
- Podaj zbiór rozwiązań nierówności
 .
.
Rysunek przedstawia fragment wykresu funkcji 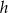 , określonej wzorem
, określonej wzorem 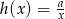 dla
dla 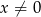 . Wiadomo, że do wykresu funkcji
. Wiadomo, że do wykresu funkcji 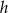 należy punkt
należy punkt 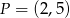 .
.
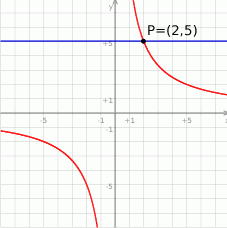
- Oblicz wartość współczynnika
 .
. - Ustal, czy liczba
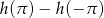 jest dodatnia czy ujemna.
jest dodatnia czy ujemna. - Rozwiąż nierówność
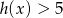 .
.
Rysunek przedstawia fragment wykresu funkcji określonej wzorem 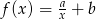 dla
dla 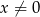 .
.
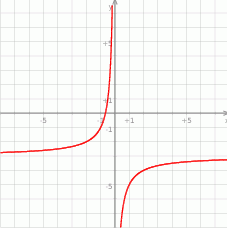
- Odczytaj z wykresu rozwiązanie nierówności
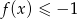 .
. - Oblicz współczynniki
 i
i 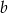 .
.

