Zestaw użytkownika nr 9403_4046
Sprawdzian - fakultet gr ALiczby rzeczywisteSuma punktów: 15
Jeśli 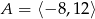 i
i 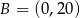 , to różnica
, to różnica 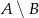 jest przedziałem
jest przedziałem
A) 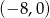 B)
B) 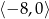 C)
C) 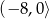 D)
D) 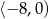
Liczba  przy dzieleniu przez 5 daje resztę 3. Liczbę
przy dzieleniu przez 5 daje resztę 3. Liczbę  można więc zapisać w postaci
można więc zapisać w postaci 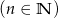
A) 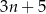 B)
B) 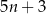 C)
C) 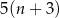 D)
D) 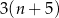
W zbiorze 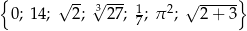
A) jest dokładnie 1 liczba wymierna
B) są dokładnie 2 liczby wymierne
C) są dokładnie 3 liczby wymierne
D) są dokładnie 4 liczby wymierne
Liczba 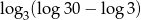 jest równa liczbie
jest równa liczbie
A) -1 B) 0 C) 1 D) 2
Wiadomo, że 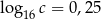 . Zatem liczba
. Zatem liczba  jest
jest
A) niewymierna B) wymierna C) większa od 2 D) mniejsza od 1
Wyrażenie 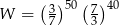 jest równe
jest równe
A) 1 B) 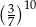 C)
C) 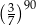 D)
D) 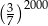
Liczbę 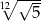 można zapisać inaczej w postaci
można zapisać inaczej w postaci
A) 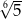 B)
B) 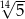 C)
C) 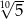 D)
D) 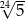
Połowę liczby  zwiększono o 20%. Otrzymano
zwiększono o 20%. Otrzymano
A) 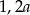 B)
B) 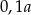 C)
C) 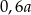 D)
D) 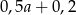
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 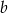 . O ile procent liczba
. O ile procent liczba 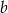 jest większa od liczby
jest większa od liczby  ?
?
A) 25% B) 80% C) 20% D) 120%
Rozwiązaniem równania 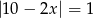 są liczby
są liczby
A) przeciwne B) różniące się o 1 C) całkowite D) niewymierne
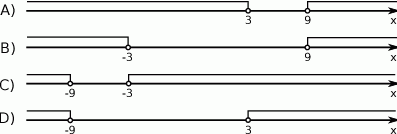
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 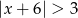 .
.
Liczba 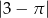 jest równa
jest równa
A) 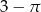 B)
B) 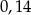 C)
C) 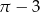 D)
D) 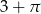
Liczba 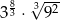 jest równa
jest równa
A) 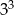 B)
B) 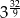 C)
C) 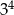 D)
D) 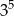
Iloczyn 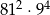 jest równy
jest równy
A) 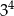 B)
B) 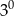 C)
C) 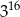 D)
D) 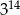
Liczbą odwrotną do 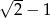 jest
jest
A) 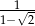 B)
B) 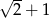 C)
C) 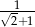 D)
D)