/Szkoła średnia/Geometria/Geometria analityczna/Parabola

Zadanie nr 9416756

Dodaj do ulubionych
Dodaj do rozwiązanych

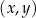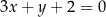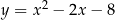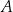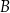W kartezjańskim układzie współrzędnych (x ,y) prosta o równaniu 3x + y + 2 = 0 przecina parabolę o równaniu y = x2 − 2x − 8 w punktach A oraz B , które są kolejnymi wierzchołkami równoległoboku 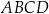ABCD . Wierzchołek 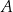A ma pierwszą współrzędną ujemną. Wierzchołek 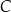C leży na prostej o równaniu 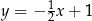1 y = − 2 x+ 1 i ma pierwszą współrzędną dodatnią. Odległość punktu 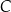C od prostej zawierającej bok 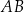AB równoległoboku jest równa 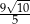√ -- 9-10- 5 . Oblicz długość boku 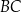BC tego równoległoboku.

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.