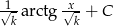Zadanie nr 9485001
Oblicz całkę 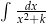 , gdzie
, gdzie 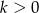 .
.
Rozwiązanie
Będziemy starali się sprowadzić daną całkę do całki 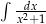 .
.
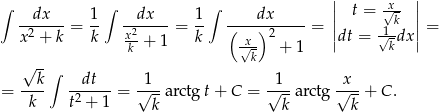
Odpowiedź: 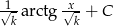
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 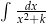 , gdzie
, gdzie 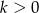 .
.
Będziemy starali się sprowadzić daną całkę do całki 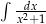 .
.
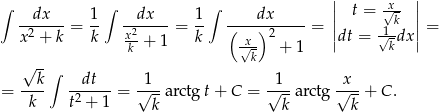
Odpowiedź: