Zestaw użytkownika nr 9489_9499
Próba przed maturą 2012poziom rozszerzonyCzas pracy: 180 min.
Dana jest funkcja 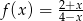 , gdzie
, gdzie 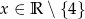 .
.
- Wyznacz wszystkie punkty należące do wykresu funkcji
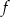 , których obie współrzędne są liczbami pierwszymi.
, których obie współrzędne są liczbami pierwszymi. - Podaj zbiór tych argumentów, dla których funkcja
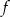 przyjmuje wartości nieujemne.
przyjmuje wartości nieujemne. - Naszkicuj wykres funkcji
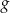 , jeśli
, jeśli 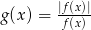 .
.
Ciąg 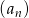 , gdzie
, gdzie 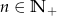 , określony jest następująco:
, określony jest następująco:
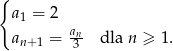
Wyznacz wszystkie wartości 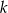 , dla których suma
, dla których suma 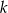 początkowych wyrazów ciągu
początkowych wyrazów ciągu 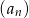 jest większa od
jest większa od 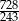 .
.
W trapezie prostokątnym 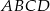 na rysunku poniżej dane są:
na rysunku poniżej dane są: 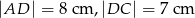 oraz
oraz 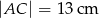 .
.
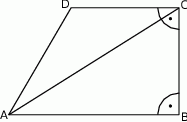
Oblicz:
- miarę kąta ostrego trapezu przy wierzchołku
 ,
, - długość odcinka łączącego środki ramion tego trapezu.
Wykaż, że jeżeli 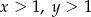 i
i 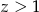 , to
, to 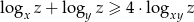 .
.
Wyznacz wszystkie wartości  , dla których ciąg
, dla których ciąg 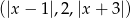 jest malejącym ciągiem arytmetycznym.
jest malejącym ciągiem arytmetycznym.
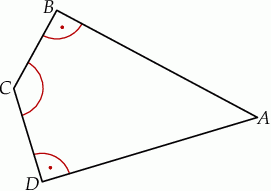
W czworokącie wypukłym 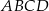 (zobacz rysunek poniżej) dane są kąty:
(zobacz rysunek poniżej) dane są kąty: 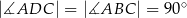 oraz
oraz 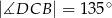 . Wykaż, że
. Wykaż, że 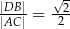 .
.
Jednym z pierwiastków wielomianu 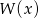 stopnia trzeciego jest liczba 1, a suma pozostałych dwóch pierwiastków jest równa 0. Do wykresu tego wielomianu należy punkt
stopnia trzeciego jest liczba 1, a suma pozostałych dwóch pierwiastków jest równa 0. Do wykresu tego wielomianu należy punkt 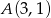 . Wiedząc, że reszta z dzielenia wielomianu
. Wiedząc, że reszta z dzielenia wielomianu 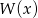 przez dwumian
przez dwumian 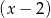 jest równa
jest równa 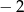 , wyznacz wzór tego wielomianu.
, wyznacz wzór tego wielomianu.
Wyznacz wszystkie wartości parametru 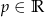 , dla których równanie
, dla których równanie 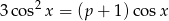 ma w przedziale
ma w przedziale 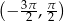 tylko trzy różne rozwiązania, z których dwa są ujemne, a jedno dodatnie.
tylko trzy różne rozwiązania, z których dwa są ujemne, a jedno dodatnie.
Ze zbioru liczb 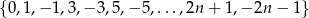 , gdzie
, gdzie  jest ustaloną liczbą naturalną, większą od 4, losujemy jednocześnie trzy liczby. Niech
jest ustaloną liczbą naturalną, większą od 4, losujemy jednocześnie trzy liczby. Niech 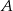 oznacza zdarzenie: suma wylosowanych liczb nie ulegnie zmianie, jeżeli w wylosowanych liczbach zmienimy znaki na przeciwne. Wiedząc, że
oznacza zdarzenie: suma wylosowanych liczb nie ulegnie zmianie, jeżeli w wylosowanych liczbach zmienimy znaki na przeciwne. Wiedząc, że 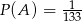 , oblicz
, oblicz  .
.
W trójkącie 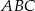 , w którym
, w którym 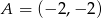 oraz
oraz 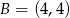 , kąt przy wierzchołku
, kąt przy wierzchołku 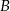 jest rozwarty. Bok
jest rozwarty. Bok 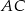 zawiera się w prostej
zawiera się w prostej 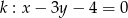 . Środek okręgu opisanego na trójkącie
. Środek okręgu opisanego na trójkącie 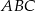 znajduje się w odległości
znajduje się w odległości 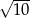 od boku
od boku 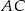 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu.
Podstawą ostrosłupa jest romb, którego pole wynosi 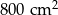 , a kąt ostry rombu ma miarę
, a kąt ostry rombu ma miarę 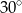 . Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz:
. Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz:
- promień tego okręgu,
- pole powierzchni bocznej ostrosłupa.

