Zestaw użytkownika nr 9532_6801

Zestaw użytkownika
nr 9532_6801

Zadanie 1

Promień i wysokość walca mają jednakową długość. Pole powierzchni bocznej wynosi 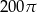200 π . Oblicz pole podstawy walca.

Zadanie 2

Przekątna przekroju osiowego walca ma długość 5 cm i jest nachylona do płaszczyzny podstawy pod kątem 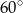60 ∘ . Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?

Zadanie 3

Długość promienia walca zmniejszono dziesięciokrotnie. Ile razy trzeba zwiększyć wysokość tego walca aby objętość się nie zmieniła?

Zadanie 4

Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 18 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 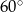60∘ . Oblicz objętość walca.

Zadanie 5

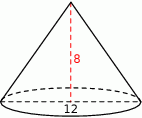
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 12. Wysokość stożka jest równa 8. Oblicz pole powierzchni bocznej tego stożka.

Zadanie 6

Stożek ma wysokość 10 cm. Pole przekroju osiowego tego stożka jest równe 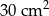30 cm 2 . Jaką długość ma tworząca tego stożka?

Zadanie 7

Oblicz objętość stożka, którego tworząca o długości 4 jest nachylona do płaszczyzny podstawy pod kątem 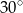30 ∘ .

Zadanie 8

Kąt rozwarcia stożka jest równy 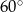∘ 60 . Promień podstawy stożka ma długość 4. Oblicz pole powierzchni bocznej stożka.

Zadanie 9

Połówkę koła o promieniu 12 zwinięto w stożek. Oblicz objętość i kąt rozwarcia tego stożka jeżeli długość łuku tej połówki koła jest obwodem podstawy, a jej promień jest tworzącą stożka.

Zadanie 10

Powierzchnia boczna stożka jest po rozwinięciu ćwiartką koła o promieniu 16 cm. Oblicz pole powierzchni całkowitej i objętość tego stożka.

Zadanie 11

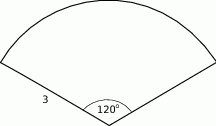
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest wycinkiem koła o promieniu 3 i kącie środkowym 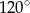120∘ (zobacz rysunek). Oblicz objętość tego stożka.

Zadanie 12

Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 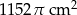2 1152π cm .

Zadanie 13

Ołowianą kulę o średnicy 60 cm przetopiono na walce o wysokości i promieniu podstawy równych 2 cm. Ile takich walców otrzymano?

Zadanie 14

Metalową kulę o promieniu 10 cm i stożek o średnicy 16 cm i wysokości 12cm przetopiono. Następnie z otrzymanego metalu wykonano walec o średnicy 8cm. Jaką wysokość ma ten walec?

Zadanie 15

Trójkąt prostokątny o przyprostokątnych 15 i 20 obraca się wokół przeciwprostokątnej. Oblicz objętość i pole powierzchni całkowitej tej bryły.

Zadanie 16

Trójkąt równoramienny o podstawie długości 6cm i ramionach długości 5cm obracamy wokół jednego z ramion. Otrzymaną w ten sposób bryłę dzielimy na dwa stożki. Podaj długość promienia podstawy i długość tworzącej każdego z tych stożków.

Zadanie 17

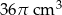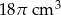Oblicz długość przeciwprostokątnej trójkąta prostokątnego, wiedząc, że objętość brył powstałych z obrotu tego trójkąta wokół przyprostokątnych wynoszą odpowiednio 36πcm 3 i 18πcm 3 .

Arkusz Wersja PDF