Zestaw użytkownika nr 9643_1870

Zestaw użytkownika
nr 9643_1870

Zadanie 1
(5 pkt)

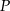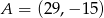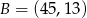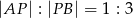Wyznacz współrzędne punktu P , który dzieli odcinek o końcach A = (29,− 15) i B = (45,13) w stosunku |AP | : |PB | = 1 : 3 .

Zadanie 2
(5 pkt)

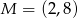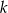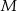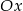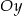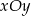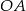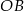Dany jest punkt M = (2 ,8 ) . Wyznacz równanie takiej prostej k , do której należy punkt M , że na ujemnej półosi Ox i dodatniej półosi Oy układu xOy prosta ta wyznacza odcinki OA i OB , których suma długości jest równa 6. Oblicz obwód trójkąta AOB .

Zadanie 3
(5 pkt)

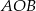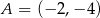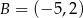Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach A = (− 2,− 4) oraz B = (− 5,2) . Jedno z jego ramion zawiera się w prostej o równaniu 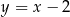y = x − 2 . Oblicz współrzędne trzeciego wierzchołka trójkąta.

Zadanie 4
(5 pkt)

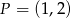Dla jakich wartości parametru α odległość punktu P = (1,2) od prostej 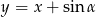y = x+ sin α jest mniejsza lub równa 1√2- .

Zadanie 5
(5 pkt)

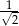Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 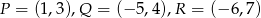P = (1,3),Q = (− 5,4),R = (− 6,7) .

Zadanie 6
(5 pkt)

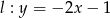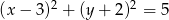Wykaż, że prosta l : y = − 2x − 1 jest styczna do okręgu 2 2 (x − 3) + (y + 2) = 5 .

Zadanie 7
(5 pkt)

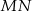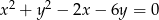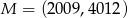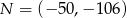Ile punktów wspólnych ma prosta MN z okręgiem 2 2 x + y − 2x − 6y = 0 jeśli M = (2009,40 12) oraz N = (− 50,− 106) .

Zadanie 8
(5 pkt)

Wyznacz równanie okręgu, który jest symetryczny do okręgu o równaniu

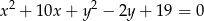
2 2 x + 10x + y − 2y + 1 9 = 0

względem prostej 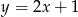y = 2x + 1 .

Zadanie 9
(5 pkt)

Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu 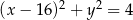(x− 16)2 + y2 = 4 jest okrąg o równaniu 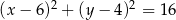(x − 6 )2 + (y − 4)2 = 1 6 , a skala tej jednokładności jest liczbą ujemną.

Zadanie 10
(5 pkt)

Przekształcenie 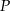P określone jest w następujący sposób: 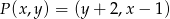P (x,y) = (y + 2,x − 1) , gdzie x ,y ∈ R .

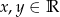  • Wykaż, że przekształcenie 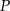P jest izometrią.
  • W prostokątnym układzie współrzędnych narysuj trójkąt o wierzchołkach 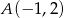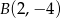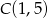A (− 1,2) , B(2,− 4) , C(1,5 ) , a następnie znajdź jego obraz w przekształceniu P .
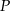  • Wyznacz równanie prostej zawierającej wysokość trójkąta 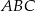ABC poprowadzoną na bok AB .
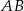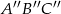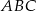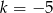  • Oblicz pole trójkąta ′′ ′′ ′′ A B C , który jest obrazem trójkąta ABC w jednokładności o środku w punkcie (0,0) i skali k = −5 .
PIC
Rozwiąż on-line Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze