Zestaw użytkownika nr 9686_1407

Zestaw użytkownika
nr 9686_1407

Zadanie 1
(2 pkt)

Obwód czworokąta wypukłego 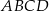ABCD jest równy 50 cm. Obwód trójkąta 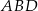ABD jest równy 46 cm, a obwód trójkąta 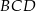BCD jest równy 36 cm. Oblicz długość przekątnej BD .

Zadanie 2
(1 pkt)

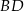Napisz wzór funkcji liniowej o współczynniku kierunkowym 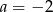a = − 2 , której wykres przecina oś 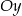Oy w punkcie 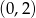(0 ,2) . Wyznacz miejsce zerowe tej funkcji.

Zadanie 3
(3 pkt)

Ewa jadąc drogą widziała elektrownię wiatrową oznaczoną na rysunku literą 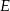E . Z punktu 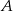A widziała ją pod kątem 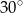30∘ stopni do kierunku drogi. A z punktu 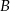B pod kątem 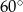60∘ . Przejeżdżając przez punkt 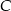C minęła elektrownię. Długość odcinka 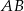AB jest równa 20km.

PIC

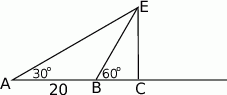
  • Oblicz miary kątów 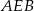AEB i BEC .
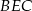  • Oblicz długość odcinka BC .
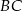  • Oblicz odległość elektrowni od drogi.

W rachunkach przyjmij, że 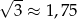√ -- 3 ≈ 1,75 .

Zadanie 4
(2 pkt)

Huta szkła produkuje kulki szklane o promieniu 5 cm. Do wysyłki będą one pakowane po 4 sztuki w sztywne pudełka w kształcie walca, którego wysokość wynosi 10 cm, a średnica 24 cm. Czy dobrze została dobrana średnica tych pudełek?

Zadanie 5
(2 pkt)

Przyprostokątne trójkąta 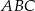ABC mają długości 10 i 24. Przeciwprostokątna trójkąta 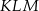KLM podobnego do niego ma długość 39. Oblicz pole trójkąta KLM .

Zadanie 6
(1 pkt)

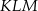Dwudziestu sześciu uczniów klasy gimnazjalnej postanowiło wybrać się na czterodniową wycieczkę z trzema noclegami. Trasa przejazdu wynosiła łącznie 600 km. W biurze turystycznym uczniowie otrzymali następujące propozycje:
– cena jednego noclegu – 25 zł od osoby
– wyżywienie w ciągu jednego dnia (śniadanie, obiad, kolacja) – 30 zł od osoby
– bilety wejściowe do muzeum i przewodnik grupy dla całej wycieczki – 1200 zł
– cena 1 km przejazdu autokarem – 2,50 zł
Oblicz łączny koszt wycieczki dla całej grupy, jeśli pierwszego dnia uczniowie mają zamiar skorzystać tylko z obiadu i kolacji, czwartego dnia tylko ze śniadania. Oblicz koszt wycieczki na jednego ucznia.

Zadanie 7
(2 pkt)

Drużyna żeglarska, płynąc po największym polskim jeziorze Śniardwy, odległość między dwiema przystaniami, która na mapie w skali 1:1 000 000 wynosi 5 cm, pokonała w czasie 2 godzin i 30 min. Oblicz średnią prędkość żaglówki.

Zadanie 8
(1 pkt)

Uprość wyrażenie 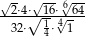√2⋅4⋅√-16⋅6√-64 32⋅√ 1⋅√41 4 .

Zadanie 9
(2 pkt)

Cena pewnego towaru wraz z 7% podatkiem VAT wynosi 69,55zł. Ile będzie kosztował ten sam towar jeżeli podatek VAT zostanie zwiększony do 22%?

Zadanie 10
(2 pkt)

Wnuczek ma tyle miesięcy co dziadek lat. Razem maja 91 lat. Ile lat ma dziadek, a ile wnuczek?

Zadanie 11
(2 pkt)

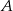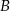Na zlecenie klienta makler ma kupić akcje spółek A i B za 1000 zł. Cena jednej akcji spółki 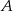A jest równa 4,25 zł, a jedna akcja spółki 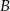B kosztuje 6,75 zł. Ile maksymalnie akcji każdego rodzaju makler może kupić, jeśli tańszych ma być o 10 więcej niż droższych?

Zadanie 12
(2 pkt)

Oblicz wysokość prostopadłościanu, którego podstawa jest prostokątem o wymiarach 3 i 4, a pole powierzchni całkowitej wynosi 94.

Zadanie 13
(2 pkt)

Oblicz pole powierzchni całkowitej i objętość prostopadłościanu 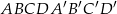ABCDA ′B′C′D ′ , w którym krawędź 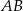AB ma długość 10 cm i tworzy z przekątną 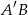A ′B ściany bocznej kąt 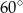60∘ , a krawędź 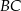BC jest o cztery centymetry krótsza od krawędzi AB .

Zadanie 14
(1 pkt)

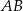Liczby 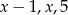x− 1,x,5 są długościami boków trójkąta równoramiennego. Oblicz x .

Zadanie 15
(3 pkt)

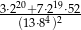Oblicz 3⋅220+-7⋅219⋅52- (13⋅84)2 .

Zadanie 16
(3 pkt)

W pierwszym miesiącu wydawnictwo sprzedawało książkę po cenie 20 zł. W drugim miesiącu cenę obniżono o 10%, co spowodowało wzrost przychodów o 8%. O ile procent więcej książek sprzedano w drugim miesiącu niż w pierwszym?

Zadanie 17
(2 pkt)

Za 4 jednakowe swetry i spodnie zapłacono 384 zł, a za sam sweter i spodnie 132 zł. Ile kosztuje sweter, a ile spodnie?

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze