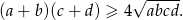Zestaw użytkownika nr 9698_1228
Zestaw użytkownika
nr 9698_1228
Okrąg o równaniu 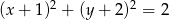 :
:
A) nie przecina osi 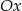 ,
,
B) nie przecina osi 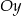 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 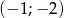 .
.
Narysowana bryła ma w podstawie kwadrat, a krawędzie boczne są prostopadłe do podstawy. Objętość tej bryły jest równa
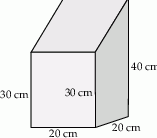
A) 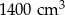 B)
B) 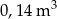 C)
C) 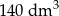 D)
D) 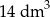
Odwrotność liczby będącej rozwiązaniem równania 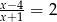 jest równa
jest równa
A) 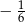 B)
B) 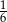 C)
C) 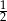 D) 6
D) 6
Cenę nart obniżono latem o 20%, a potem jeszcze o 15%. Po tych dwóch obniżkach narty kosztowały 705 zł i 50 gr. Wynika z tego, że pierwotna cena nart to
A) 1037,5 zł B) 1100 zł C) 952,42 zł D) 980 zł
Ciąg 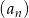 jest określony wzorem
jest określony wzorem 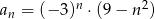 dla
dla 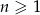 . Wynika stąd, że
. Wynika stąd, że
A) 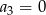 B)
B) 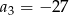 C)
C) 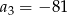 D)
D) 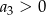
Wiadomo, że tangens kąta ostrego  jest równy
jest równy  . Wobec tego:
. Wobec tego:
A) 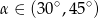 B)
B) 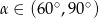 C)
C) 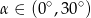 D)
D) 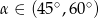
W okręgu o środku w punkcie 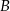 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 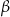 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 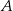 i
i 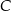 leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta
leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta 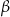 znajduje się w punkcie
znajduje się w punkcie 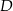 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 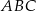 jest równoboczny
jest równoboczny
B) 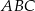 jest prostokątny
jest prostokątny
C) 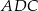 jest prostokątny
jest prostokątny
D) 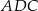 jest równoboczny
jest równoboczny
Wyrażenie 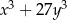 jest równe iloczynowi
jest równe iloczynowi
A) 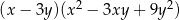
B) 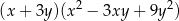
C) 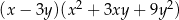
D) 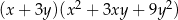
Stosunek pól dwóch kół jest równy 9. Wynika stąd, że promień większego koła jest większy od promienia mniejszego koła
A) o 3 B) 9 razy C) 3 razy D) o 9
Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 45% B) 63% C) 22% D) 33%
Trzeci wyraz ciągu geometrycznego jest równy 4, a czwarty wyraz tego ciągu jest równy -2. Pierwszy wyraz tego ciągu jest równy
A) -8 B) 8 C) 16 D) -16
Dane są wielomiany 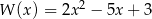 i
i 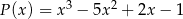 . Wielomian
. Wielomian 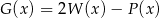 jest równy
jest równy
A) 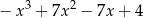 B)
B) 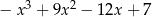 C)
C) 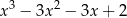 D)
D) 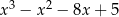
Odległość liczby  od liczby -8 na osi liczbowej jest równa
od liczby -8 na osi liczbowej jest równa
A) 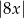 B)
B) 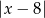 C)
C) 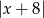 D)
D) 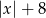
Wśród pewnej grupy pracowników przeprowadzono ankietę, w której odpowiadano na pytanie „Ile godzin dziennie spędzasz w pracy?”. Wyniki ankiety przedstawiono w tabeli.
| Liczba osób | 6 | 10 | 4 |
| Czas w godzinach | 7 | 8 | 9 |
Średnia liczba godzin spędzonych w pracy w tej grupie wynosi około
A) 10 B) 7 C) 9 D) 8
Środek  okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 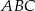 należy do boku
należy do boku 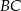 . Suma miar kątów
. Suma miar kątów 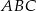 i
i 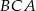 trójkąta
trójkąta 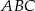 jest równa
jest równa
A) 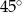 B)
B) 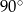 C)
C) 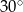 D)
D) 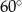
Liczba 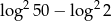 jest równa
jest równa
A) 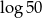 B)
B) 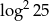 C)
C) 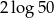 D)
D) 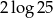
Przekątna prostopadłościanu o wymiarach 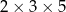 ma długość
ma długość
A) 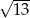 B)
B) 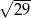 C)
C) 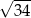 D)
D) 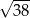
Dane są zbiory 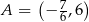 i
i 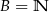 liczb naturalnych dodatnich. Wówczas iloczyn zbiorów
liczb naturalnych dodatnich. Wówczas iloczyn zbiorów 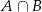 jest równy
jest równy
A) 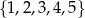 B)
B) 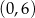 C)
C) 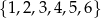 D)
D) 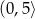
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 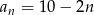 , gdzie
, gdzie 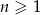 jest równa 14. Zatem
jest równa 14. Zatem
A) 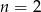 B)
B) 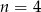 C)
C) 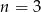 D) liczba
D) liczba 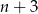 dzieli się przez 5
dzieli się przez 5
Przybliżona długość przeciwprostokątnej trójkąta prostokątnego przedstawionego na rysunku jest równa

A) 5,85 B) 5,49 C) 5,9 D) 5,5
Iloraz liczb 5670 i 6615 jest równy
A)  B)
B) 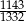 C)
C) 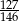 D)
D) 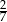
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 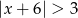 .
.
Prawdopodobieństwo zdarzenia 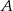 jest równe
jest równe 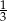 , a prawdopodobieństwo sumy zdarzeń
, a prawdopodobieństwo sumy zdarzeń 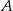 i
i 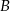 jest równe
jest równe 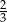 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 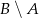 jest równe
jest równe
A)  B)
B) 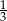 C)
C)  D)
D) 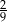
Liczba przekątnych wielokąta wypukłego jest 4 razy większa od liczby jego boków. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 10 B) 11 C) 9 D) 8
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 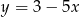 jest równy
jest równy
A) 3 B) 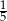 C)
C) 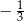 D) -5
D) -5
Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.
Suma dwóch liczb jest równa 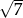 , a ich różnica
, a ich różnica 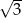 . Oblicz iloczyn tych liczb.
. Oblicz iloczyn tych liczb.
W roku 2005 na uroczystości urodzin zapytano jubilata, ile ma lat. Jubilat odpowiedział: „Jeśli swój wiek sprzed 10 lat pomnożę przez swój wiek za 11 lat, to otrzymam rok mojego urodzenia". Ułóż odpowiednie równanie, rozwiąż je i zapisz, w którym roku urodził się ten jubilat.
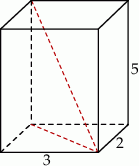
Podstawą ostrosłupa 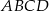 jest trójkąt
jest trójkąt 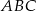 . Krawędź
. Krawędź 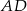 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek).
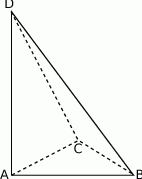
Oblicz objętość ostrosłupa 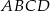 , jeśli wiadomo, że
, jeśli wiadomo, że 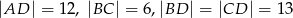 .
.
W kulę o promieniu długości 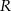 wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
Spośród wyrazów skończonego ciągu arytmetycznego 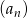 danego wzorem
danego wzorem 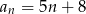 , gdzie
, gdzie 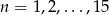 wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
Uzasadnij, że jeżeli 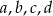 są liczbami dodatnimi to
są liczbami dodatnimi to