Zestaw użytkownika nr 9712_8923

Zestaw użytkownika
nr 9712_8923

Zadanie 1

W pudełku zmieszano 30 ziaren fasoli, 20 ziaren ciecierzycy i 50 ziaren grochu.

  • Losujemy jedno ziarenko. Jakie jest prawdopodobieństwo wylosowania ziarenka ciecierzycy?
  • Jako pierwsze wylosowano ziarenko fasoli. Jakie jest prawdopodobieństwo, że drugim wylosowanym ziarenkiem nie będzie ziarenko fasoli?
  • Z pudełka usunięto po 10% ziarenek każdego rodzaju. Jakie jest prawdopodobieństwo wylosowania ziarenka fasoli?
Zadanie 2

Każdej karcie bankomatowej jest przypisany numer identyfikacyjny zwany kodem PIN. Kod ten składa się z czterech cyfr (cyfry mogą się powtarzać, ale kodem PIN nie może być 0000). Oblicz prawdopodobieństwo, że w losowo utworzonym kodzie PIN żadna cyfra się nie powtórzy. Wynik podaj w postaci ułamka nieskracalnego.

Zadanie 3

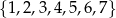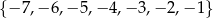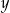Ze zbioru {1,2,3,4 ,5 ,6,7} losujemy liczbę x , a ze zbioru {− 7 ,−6 ,−5 ,−4 ,−3 ,−2 ,−1 } liczbę y . Oblicz prawdopodobieństwo tego, że x + y > 0 .

Zadanie 4

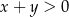Dane są trzy sześcienne kostki do gry: czerwona, niebieska i zielona. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przy jednokrotnym rzucie trzema kostkami liczba otrzymana na niebieskiej kostce jest większa niż suma liczb otrzymanych na dwóch pozostałych kostkach.

Zadanie 5

Strzelając do tarczy pewien strzelec uzyskuje co najmniej 9 punktów z prawdopodobieństwem 0,5, a co najwyżej 9 punktów z prawdopodobieństwem 0,7. Oblicz prawdopodobieństwo, że ten strzelec uzyska dokładnie 9 punktów.

Zadanie 6

W pewnej grupie uczniów każdy zna język angielski lub niemiecki. Wiadomo, że prawdopodobieństwo wylosowania z tej grupy ucznia znającego język angielski jest równe 78 , natomiast prawdopodobieństwo wylosowania ucznia znającego język niemiecki jest równe 4 5 . Jakie jest prawdopodobieństwo tego, że losowo wybrany uczeń zna obydwa języki?

Zadanie 7

W jednej szufladzie znajdują się 3 szaliki czarne i 4 szaliki niebieskie, a w drugiej szufladzie są 2 czapki czarne i 1 niebieska. Wyjmujemy losowo jeden szalik i jedną czapkę. Które prawdopodobieństwo jest większe: zdarzenia 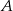A , że otrzymamy komplet w jednym kolorze, czy zdarzenia 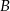B , że otrzymamy czapkę i szalik w różnych kolorach? Odpowiedź uzasadnij, wykonując odpowiednie obliczenia.

Zadanie 8

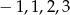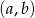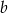W pudełku są cztery kartki, na których wypisano liczby − 1,1,2,3 (na każdej kartce jedną liczbę). Losujemy jedną kartkę, zapisujemy liczbę i zwracamy kartkę do pudełka. Następnie losujemy drugą kartkę i zapisujemy liczbę. Wylosowane liczby tworzą parę (a,b) , gdzie a jest liczbą wylosowaną za pierwszym razem, zaś b liczbą wylosowaną za drugim razem. Oblicz prawdopodobieństwo zdarzenia

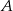  • A – iloczyn wylosowanych liczb jest liczbą pierwszą;
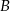  • B – różnica wylosowanych liczb jest liczbą parzystą.
Zadanie 9

W pewnej klasie okazało się, że są 3 osoby, które urodziły się w kwietniu tego samego roku i są dwie osoby, które urodziły się w lipcu tego samego roku. Oblicz prawdopodobieństwo, że troje z tych 5 uczniów urodziło się tego samego dnia roku.

Zadanie 10

Poniższy diagram przedstawia wyniki ankiety znajomości języków obcych wśród uczniów pewnej szkoły.

PIC

Oblicz prawdopodobieństwo, że losowo wybrana osoba z ankietowanych zna

  • język angielski,
  • co najmniej jeden język obcy.
Zadanie 11

Listonosz losowo rozmieszcza 4 listy w 6 skrzynkach na listy. Jakie jest prawdopodobieństwo, że przynajmniej dwa listy znajdą się w tej samej skrzynce?

Zadanie 12

Ze zbioru liczb całkowitych spełniających nierówność 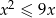2 x ≤ 9x losujemy dwie różne liczby. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo wylosowania dwóch liczb pierwszych.

Zadanie 13

Ze zbioru liczb naturalnych spełniających nierówność 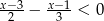x−-3- x−1- 2 − 3 < 0 losujemy dwie różne liczby 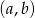(a,b) . Oblicz prawdopodobieństwo zdarzenia: punkt o współrzędnych 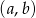(a,b ) należy do wykresu funkcji y = x + 4 .

Zadanie 14

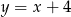Przedstawiono informacje dotyczące znajomości języka angielskiego oraz języka niemieckiego w pewnej 200 osobowej grupie studentów:
25% studentów zna język angielski i język niemiecki,
50% studentów zna język niemiecki,
60% zna język angielski.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany z tej grupy student

  • zna język angielski i nie zna języka niemieckiego,
  • nie zna języka angielskiego i nie zna języka niemieckiego.
Zadanie 15

Windą, zatrzymującą się na 6 piętrach, jadą 4 osoby. Jakie jest prawdopodobieństwo tego, że każda osoba wysiądzie na innym piętrze?

Zadanie 16

W pewnej szkole 20% uczniów uczęszcza na kółko plastyczne, a 34% uczniów uczęszcza na kółko muzyczne. Wiadomo ponadto, że 58% uczniów nie uczęszcza na żadne z tych kółek. Oblicz jakie jest prawdopodobieństwo, że losowy wybrany uczeń tej szkoły uczęszcza jednocześnie na kółko plastyczne i muzyczne.

Zadanie 17

Rzucamy 3 razy kostką do gry. Oblicz prawdopodobieństwo, że kolejno otrzymane liczby utworzą ciąg arytmetyczny.

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze