Zestaw użytkownika nr 9789_1499

Zestaw użytkownika
nr 9789_1499

Zadanie 1
(5 pkt)

Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia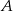
A – na każdej kostce wypadła nieparzysta liczba oczek,
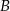B – suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 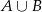A ∪ B .

Zadanie 2
(5 pkt)

Danych jest osiem kul z numerami od 1 do 8, oraz dziesięć szuflad z numerami od 1 do 10. Rozmieszczamy w dowolny sposób kule w szufladach. Oblicz prawdopodobieństwa następujących zdarzeń:

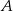  • A – wszystkie kule znajdą się w szufladach z numerami parzystymi.
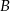  • B – dokładnie dwie szuflady pozostaną puste.
Zadanie 3
(5 pkt)

Spośród wyrazów skończonego ciągu arytmetycznego 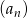(an) danego wzorem 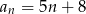an = 5n + 8 , gdzie 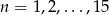n = 1,2,...,15 wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.

Zadanie 4
(5 pkt)

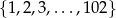Ze zbioru {1,2,3,...,102} losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?

Zadanie 5
(5 pkt)

Dany jest wielomian 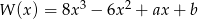3 2 W (x) = 8x − 6x + ax+ b . Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.

Zadanie 6
(2 pkt)

Z urny, w której jest 6 kul czarnych i 4 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule jednakowych kolorów.

Zadanie 7
(5 pkt)

W pudełku zmieszano 30 ziaren fasoli, 20 ziaren ciecierzycy i 50 ziaren grochu.

  • Losujemy jedno ziarenko. Jakie jest prawdopodobieństwo wylosowania ziarenka ciecierzycy?
  • Jako pierwsze wylosowano ziarenko fasoli. Jakie jest prawdopodobieństwo, że drugim wylosowanym ziarenkiem nie będzie ziarenko fasoli?
  • Z pudełka usunięto po 10% ziarenek każdego rodzaju. Jakie jest prawdopodobieństwo wylosowania ziarenka fasoli?
Zadanie 8
(2 pkt)

Każdej karcie bankomatowej jest przypisany numer identyfikacyjny zwany kodem PIN. Kod ten składa się z czterech cyfr (cyfry mogą się powtarzać, ale kodem PIN nie może być 0000). Oblicz prawdopodobieństwo, że w losowo utworzonym kodzie PIN żadna cyfra się nie powtórzy. Wynik podaj w postaci ułamka nieskracalnego.

Zadanie 9
(5 pkt)

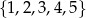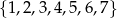Dane są zbiory liczb całkowitych: {1,2,3,4 ,5 } i {1,2,3,4 ,5,6,7} . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.

Zadanie 10
(5 pkt)

W koszu znajdują się owoce: 12 jabłek i 8 pomarańczy. Wyjmujemy kolejno trzy owoce, nie odkładając ich do kosza. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwie pomarańcze.

Zadanie 11
(5 pkt)

W urnie znajdują się jedynie kule białe i czarne. Kul białych jest trzy razy więcej niż czarnych. Oblicz, ile jest kul w urnie, jeśli przy jednoczesnym losowaniu dwóch kul prawdopodobieństwo otrzymania kul o różnych kolorach jest większe od 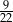-9 22 .

Zadanie 12
(5 pkt)

Na loterii jest 40 losów, w tym 4 wygrywające. Kupujemy 2 losy. Jakie jest prawdopodobieństwo tego, że będzie wśród nich dokładnie jeden los wygrywający?

Zadanie 13
(5 pkt)

Przeprowadzono badania, dotyczące liczby osób jadących w samochodach osobowych w godzinach rannych, w kierunku centrum pewnego miasta. Wyniki badań przedstawione są na digramie kołowym.

PIC

  • Oblicz średnią liczbę osób jadących w samochodzie osobowym w godzinach rannych w kierunku centrum.
  • Oblicz prawdopodobieństwo, że w losowo wybranym samochodzie osobowym, w godzinach rannych, w kierunku centrum, były więcej niż 3 osoby.
  • Wiedząc, że samochodów osobowych, w których były 4 osoby, zaobserwowano o 350 więcej, niż samochodów w których było 5 osób, oblicz, ile wszystkich samochodów obserwowano w trakcie badań.
Zadanie 14
(5 pkt)

Z pojemnika, w którym są dwa losy wygrywające i trzy losy puste, losujemy dwa razy po jednym losie bez zwracania. Oblicz prawdopodobieństwo, że otrzymamy co najmniej jeden los wygrywający. Wynik przedstaw w postaci ułamka nieskracalnego.

Zadanie 15
(5 pkt)

Spośród liczb naturalnych trzycyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, która przy dzieleniu przez 11 daje resztę 3.

Zadanie 16
(5 pkt)

Z sześciu odcinków długości 1,3,5,6,7,9 wybieramy losowo trzy. Oblicz prawdopodobieństwo że można z nich zbudować trójkąt.

Zadanie 17
(5 pkt)

W wazonie stoi 12 czerwonych i 8 żółtych róż. Pani Krystyna wyjęła losowo dwie róże z wazonu. Oblicz prawdopodobieństwo, że wśród wybranych kwiatów jest przynajmniej jedna róża żółta.

Zadanie 18
(5 pkt)

W garderobie pani Joanny wiszą 3 żakiety: biały, zielony i granatowy oraz 4 spódnice: czarna, biała, granatowa i szara. Oblicz prawdopodobieństwo zdarzenia, że wybierając losowo jeden żakiet i jedną spódnicę, pani Joanna skompletuje strój w jednym kolorze.

Zadanie 19
(5 pkt)

Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 12.

Zadanie 20
(5 pkt)

Ze zbioru liczb 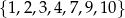{1,2,3,4 ,7 ,9,10} losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.

Zadanie 21
(5 pkt)

W urnie znajduję się 5 kul białych i 3 czarne. Wyjmujemy losowo 4 kule. Oblicz prawdopodobieństwo, że wśród wyjętych są przynajmniej 2 kule czarne.

Zadanie 22
(5 pkt)

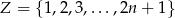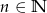Ze zbioru Z = { 1,2,3,...,2n + 1} , gdzie n ∈ N wylosowano równocześnie dwie liczby. Wyznacz n , tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od 713- .

Zadanie 23
(5 pkt)

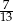Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że w każdym rzucie otrzymamy inną liczbę oczek.

Zadanie 24
(5 pkt)

W dwóch pudełkach są cukierki. W pierwszym pudełku jest 15 cukierków czekoladowych i 5 owocowych, a w drugim pudełku jest 20 cukierków czekoladowych i 30 cukierków owocowych. Losujemy cukierek najpierw z pierwszego, a potem z drugiego pudełka. Jakie jest prawdopodobieństwo, że w wyniku losowania otrzymamy dwa cukierki czekoladowe?

Zadanie 25
(5 pkt)

W urnie jest pewna liczba kul białych i pewna liczba kul czarnych – razem 9 kul. Ile jest kul białych w urnie, jeśli wiadomo, że przy jednoczesnym losowaniu dwóch kul z tej urny prawdopodobieństwo otrzymania kul tego samego koloru jest równe prawdopodobieństwu otrzymania kul różnych kolorów?

Zadanie 26
(5 pkt)

Z talii pięćdziesięciu dwu kart wyciągnięto losowo trzy karty. Oblicz prawdopodobieństwo wyciągnięcia dokładnie jednego króla.

Zadanie 27
(5 pkt)

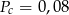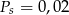Przy produkcji pewnego wyrobu wykonuje się dwie kolejno następujące po sobie operacje: cięcie i szlifowanie. Prawdopodobieństwa uszkodzenia obrabianego elementu w każdej z tych operacji wynoszą odpowiednio Pc = 0,08 i Ps = 0,02 .

  • Oblicz prawdopodobieństwo, że podany obróbce element zostanie uszkodzony.
  • Ile powinno wynosić prawdopodobieństwo 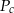Pc by prawdopodobieństwo uszkodzenia elementu w trakcie obróbki wynosiło mniej niż 0,069?
Zadanie 28
(5 pkt)

Ile maksymalnie kul zielonych można włożyć do urny, w której jest 7 kul czerwonych, aby prawdopodobieństwo wylosowania 2 kul różnokolorowych było większe lub równe 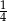14 ?

Zadanie 29
(5 pkt)

Spośród liczb 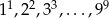1 2 3 9 1 ,2 ,3 ,...,9 wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.

Zadanie 30
(5 pkt)

10 kul rozmieszczamy w 10 szufladach. Jakie jest prawdopodobieństwo tego, że każda szuflada będzie zajęta?

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze