Zestaw użytkownika nr 9792_3843

Zestaw użytkownika
nr 9792_3843

Zadanie 1

(5 pkt)

Uzasadnij, że dla każdej liczby 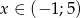x ∈ (− 1;5) wyrażenie 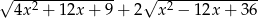√ --2----------- √ --2----------- 4x + 12x + 9 + 2 x − 12x + 36 ma stałą wartość.

Zadanie 2

(5 pkt)

Uprość wyrażenie 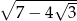∘ -----√--- 7 − 4 3 .

Zadanie 3

(5 pkt)

Suma dwóch liczb jest równa 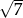√ -- 7 , a ich różnica 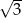√ -- 3 . Oblicz iloczyn tych liczb.

Zadanie 4

(5 pkt)

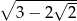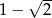Uzasadnij, że liczby ∘ -----√--- 3 − 2 2 i √ -- 1 − 2 są liczbami przeciwnymi.

Zadanie 5

(5 pkt)

Na osi liczbowej zaznaczono przedział 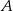złożony z tych liczb rzeczywistych, których odległość od punktu 1 jest niewiększa od 4,5. Przedział 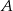przesunięto wzdłuż osi o 2 jednostki w kierunku dodatnim, otrzymując przedział 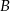. Wyznacz wszystkie liczby całkowite, które należą jednocześnie do 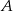i do .

Zadanie 6

(5 pkt)

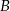Wykaż, że suma kwadratów dwóch kolejnych liczb nieparzystych nie dzieli się przez 4.

Zadanie 7

(5 pkt)

Wykaż, że liczba 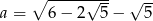∘ -----√--- √ -- a = 6 − 2 5 − 5 jest całkowita.

Zadanie 8

(5 pkt)

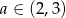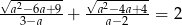Wykaż, że dla a ∈ (2,3) zachodzi równość √a-2−-6a+9 √a-2−-4a+-4 3−a + a−2 = 2 .

Zadanie 9

(5 pkt)

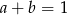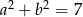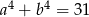Uzasadnij, że jeżeli a + b = 1 i 2 2 a + b = 7 , to 4 4 a + b = 31 .

Zadanie 10

(5 pkt)

Wykaż, że liczba 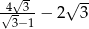-4√3- √ -- √3− 1 − 2 3 jest liczbą wymierną.

Zadanie 11

(5 pkt)

Doprowadź wyrażenie 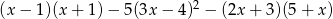2 (x − 1)(x + 1) − 5(3x − 4) − (2x + 3)(5+ x) do najprostszej postaci, a następnie oblicz jego wartość dla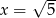 √ -- x = 5

Zadanie 12

(5 pkt)

Oblicz 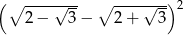(∘ ---√---- ∘ ----√--)2 2− 3 − 2+ 3 .

Arkusz Wersja PDF