Zestaw użytkownika nr 9948_2104
zadania optymalizacyjne 2
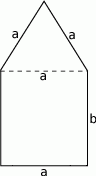
Obwód okna przedstawionego na rysunku wynosi 7 m. W jakim stosunku powinny pozostawać odcinki  i
i 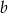 , aby przez okno wpadało jak najwięcej światła?
, aby przez okno wpadało jak najwięcej światła?
Obwód trójkąta równobocznego 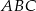 jest równy 12 cm. Punkty
jest równy 12 cm. Punkty 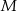 ,
, 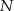 i
i 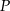 należą odpowiednio do boków
należą odpowiednio do boków 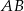 ,
, 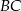 ,
, 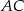 tego trójkąta przy czym
tego trójkąta przy czym 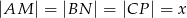 . Zbadaj dla jakiej wartości
. Zbadaj dla jakiej wartości  , pole trójkąta
, pole trójkąta 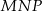 będzie najmniejsze. Znajdź wartość tego pola.
będzie najmniejsze. Znajdź wartość tego pola.
Dany jest zbiór wszystkich graniastosłupów prawidłowych sześciokątnych, których suma długości wszystkich krawędzi jest równa 216. Oblicz długość krawędzi podstawy i wysokość tego z danych graniastosłupów, który ma największe pole powierzchni bocznej.
Jaką największą objętość ma walec wpisany w kulę o średnicy długości 12 cm?
W stożek, którego wysokość ma długość 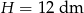 , a promień jego podstawy ma długość
, a promień jego podstawy ma długość 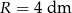 wpisano walec, o podstawach równoległych do podstawy stożka. Jakie powinny być wymiary walca, aby jego objętość była największa?
wpisano walec, o podstawach równoległych do podstawy stożka. Jakie powinny być wymiary walca, aby jego objętość była największa?
Suma długości wysokości i długości jednej krawędzi podstawy graniastosłupa prawidłowego czworokątnego jest równa 2. Jaką najmniejszą długość może mieć przekątna takiego graniastosłupa.
Spośród tych graniastosłupów prawidłowych trójkątnych, których suma długości wszystkich krawędzi jest równa 18, wybierz graniastosłup o największej objętości. Oblicz tę maksymalną objętość.
Puszka konserwy ma kształt walca. Jaką wysokość i jaki promień podstawy powinna mieć ta puszka, aby przy objętości puszki 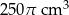 zużyć jak najmniej materiału na jej wykonanie.
zużyć jak najmniej materiału na jej wykonanie.
Dany jest ciąg arytmetyczny 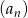 dla
dla 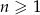 , w którym
, w którym 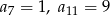 .
.
- Oblicz pierwszy wyraz
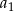 i różnicę
i różnicę  ciągu
ciągu 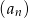 .
. - Sprawdź, czy ciąg
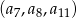 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 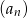 miała wartość najmniejszą.
miała wartość najmniejszą.
Pierwszy, trzeci i jedenasty wyraz ciągu arytmetycznego o różnicy 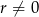 są kolejnymi wyrazami ciągu geometrycznego o ilorazie
są kolejnymi wyrazami ciągu geometrycznego o ilorazie 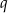 . Dla jakich wartości parametru
. Dla jakich wartości parametru 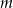 funkcja
funkcja 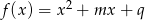 osiąga minimum większe od -196?
osiąga minimum większe od -196?
Dziesiąty wyraz ciągu arytmetycznego 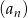 jest o 48 mniejszy od sumy jego pierwszych 7 wyrazów. Oblicz sumę pierwszych 33 wyrazów tego ciągu wiedząc, że iloczyn
jest o 48 mniejszy od sumy jego pierwszych 7 wyrazów. Oblicz sumę pierwszych 33 wyrazów tego ciągu wiedząc, że iloczyn 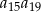 ma najmniejszą możliwą wartość.
ma najmniejszą możliwą wartość.
Ciąg 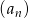 jest ciągiem arytmetycznym, w którym
jest ciągiem arytmetycznym, w którym 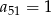 oraz wyrażanie
oraz wyrażanie 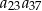 ma najmniejszą możliwą wartość. Wyznacz
ma najmniejszą możliwą wartość. Wyznacz 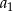 .
.
Wyznacz dziedzinę i najmniejszą wartość funkcji 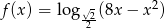 .
.
Dana jest funkcja 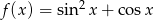 dla
dla 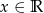 .
.
- Rozwiąż równanie
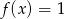 w przedziale
w przedziale 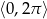 .
. - Wyznacz największą wartość funkcji
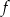 .
.
Dla każdej liczby rzeczywistej  obliczamy różnicę sześcianów liczb: o 1 mniejszej od
obliczamy różnicę sześcianów liczb: o 1 mniejszej od  oraz o 2 większej od
oraz o 2 większej od  . Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
. Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
Wyznacz największą wartość funkcji 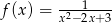 .
.
Wyznacz największą wartość funkcji 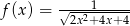 .
.
Wyznacz najmniejszą i największą wartość funkcji 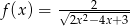 na przedziale
na przedziale 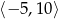 .
.
Wyznacz tę wartość parametru 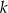 , dla której suma kwadratów pierwiastków równania
, dla której suma kwadratów pierwiastków równania 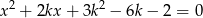 jest największa z możliwych.
jest największa z możliwych.
Funkcja kwadratowa postaci 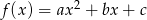 , posiada miejsca zerowe równe -3 i 2, a jej współczynnik
, posiada miejsca zerowe równe -3 i 2, a jej współczynnik 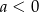 . Oblicz wartości współczynników
. Oblicz wartości współczynników 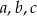 wiedząc, ze największa wartość funkcji wynosi
wiedząc, ze największa wartość funkcji wynosi 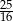 .
.

