Zestaw użytkownika nr 9959_4329

Zestaw użytkownika
nr 9959_4329

Zadanie 1

Ania przeczytała książkę science-ﬁction, która miała 572 strony. Ania każdego dnia czytała o taką samą liczbę stron więcej, niż w dniu poprzednim. Ile dni Ania czytała tę książkę, jeżeli wiadomo, że w trzecim dniu Ania przeczytała 28 stron, a w ostatnim 68?

Zadanie 2

Długości boków trójkąta tworzą ciąg geometryczny. Jaki warunek spełniać musi iloraz tego ciągu?

Zadanie 3

Długości boków trójkąta są kolejnymi wyrazami rosnącego ciągu geometrycznego o ilorazie 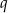, a cosinus jednego z jego kątów jest równy q − 4 .

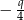Wyznacz .
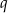Wiedząc, że promień okręgu opisanego na tym trójkącie ma długość 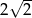, oblicz pole tego trójkąta.

Zadanie 4

Dla jakich wartości parametru 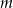dziedziną funkcji 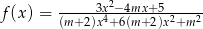-----3x2−4mx+-5----- f(x ) = (m+2)x4+6(m+ 2)x2+m 2 jest zbiór liczb rzeczywistych?

Zadanie 5

Naszkicuj wykres funkcji 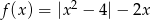2 f (x) = |x − 4|− 2x . Określ liczbę rozwiązań równania 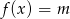f (x) = m w zależności od wartości parametru .

Zadanie 6

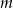Znajdź zbiór środków wszystkich okręgów stycznych wewnętrznie do okręgu o równaniu 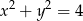x2 + y2 = 4 i stycznych do prostej o równaniu y = 0 .

Zadanie 7

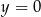Ramiona kąta ostrego o mierze 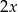przecięto prostą 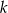prostopadłą do dwusiecznej kąta, która jest odległa o 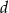od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej 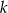. Oblicz odległość środków tych okręgów.

Zadanie 8

Odległość środka wysokości ostrosłupa prawidłowego trójkątnego od ściany bocznej jest równa 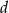. Krawędź boczna tworzy z płaszczyzną podstawy kąt . Oblicz objętość i pole powierzchni całkowitej ostrosłupa.

Zadanie 9

Miara kąta między ramionami trójkąta równoramiennego o polu 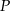jest równa . Oblicz promień okręgu wpisanego w ten trójkąt.

Arkusz Wersja PDF