Zestaw użytkownika nr 9976_5999
Matura z matematyki Poziom PodstawowyARKUSZ ICzas pracy: 170 min.Suma punktów: 50
Rozwiązaniem równania 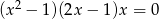 nie jest liczba
nie jest liczba
A) 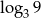 B)
B) 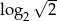 C)
C) 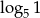 D)
D) 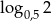
Wyrażenie 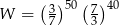 jest równe
jest równe
A) 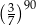 B)
B) 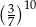 C)
C) 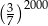 D) 1
D) 1
Stosunek miar kątów czworokąta jest równy 1:2:3:4. Zatem najmniejszy kąt tego wielokąta ma miarę
A) 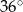 B)
B) 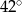 C)
C) 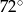 D)
D) 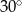
Wskaż 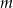 , dla którego funkcja liniowa
, dla którego funkcja liniowa 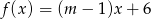 jest rosnąca
jest rosnąca
A) 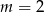 B)
B) 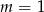 C)
C) 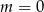 D)
D) 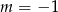
Narysowana bryła ma w podstawie kwadrat, a krawędzie boczne są prostopadłe do podstawy. Objętość tej bryły jest równa
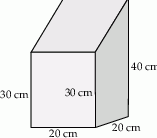
A) 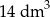 B)
B) 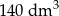 C)
C) 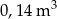 D)
D) 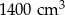
Okrąg o równaniu 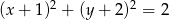 :
:
A) nie przecina osi 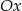 ,
,
B) nie przecina osi 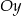 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 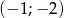 .
.
Odwrotność liczby będącej rozwiązaniem równania 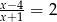 jest równa
jest równa
A) 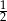 B) 6 C)
B) 6 C) 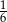 D)
D) 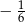
Funkcja 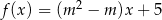 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 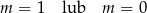 B)
B) 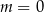 C)
C) 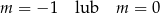 D)
D) 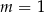
Wskaż nierówność, którą spełnia liczba 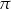 .
.
A) 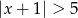 B)
B) 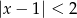 C)
C) 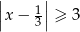 D)
D) 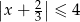
Ciąg 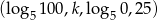 jest arytmetyczny. Wobec tego
jest arytmetyczny. Wobec tego
A) 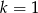 B)
B) 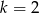 C)
C) 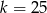 D)
D) 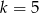
Liczba 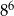 jest większa od liczby
jest większa od liczby 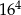
A) o 300% B) o 200% C) o 400% D) o 100%
Liczba 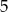 nie należy do dziedziny wyrażenia
nie należy do dziedziny wyrażenia
A) 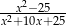 B)
B) 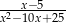 C)
C) 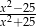 D)
D) 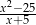
Jeżeli 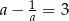 to liczba
to liczba 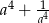 jest równa
jest równa
A) 119 B) 123 C) 81 D) 121
Ciąg 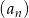 jest określony wzorem
jest określony wzorem 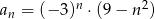 dla
dla 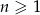 . Wynika stąd, że
. Wynika stąd, że
A) 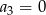 B)
B) 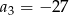 C)
C) 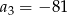 D)
D) 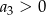
Wiadomo, że tangens kąta ostrego  jest równy
jest równy  . Wobec tego:
. Wobec tego:
A) 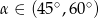 B)
B) 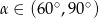 C)
C) 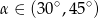 D)
D) 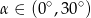
Kąty wewnętrzne przy wierzchołkach 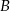 i
i 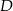 trapezu
trapezu 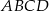 są równe odpowiednio
są równe odpowiednio 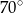 i
i 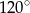 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 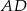 i
i 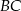 przecinają się pod kątem
przecinają się pod kątem
A) 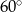 B)
B) 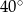 C)
C) 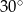 D)
D) 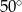
W okręgu o środku w punkcie 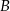 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 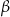 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 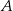 i
i 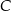 leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta
leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta 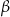 znajduje się w punkcie
znajduje się w punkcie 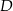 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 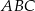 jest prostokątny
jest prostokątny
B) 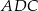 jest prostokątny
jest prostokątny
C) 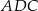 jest równoboczny
jest równoboczny
D) 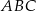 jest równoboczny
jest równoboczny
Ciągiem geometrycznym jest ciąg określony wzorem
A) 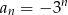 B)
B) 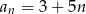 C)
C) 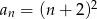 D)
D) 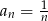
Osią symetrii paraboli będącej wykresem funkcji 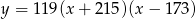 jest prosta o równaniu
jest prosta o równaniu
A) 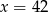 B)
B) 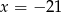 C)
C) 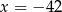 D)
D) 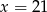
Liczbę 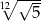 można zapisać inaczej w postaci
można zapisać inaczej w postaci
A) 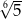 B)
B) 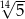 C)
C) 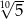 D)
D) 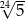
Wyrażenie 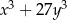 jest równe iloczynowi
jest równe iloczynowi
A) 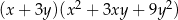
B) 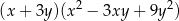
C) 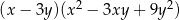
D) 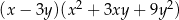
Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 22% B) 63% C) 45% D) 33%
Stosunek pól dwóch kół jest równy 9. Wynika stąd, że promień większego koła jest większy od promienia mniejszego koła
A) o 3 B) o 9 C) 9 razy D) 3 razy
Na rysunku przedstawiono wykres funkcji 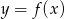 .
.
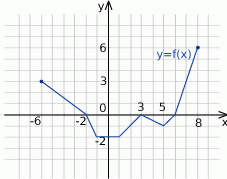
Zbiorem wartości funkcji 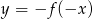 jest
jest
A) 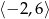 B)
B) 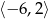 C)
C) 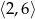 D)
D) 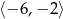
Kąt rozwarcia stożka ma miarę 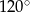 , a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 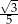 B)
B) 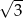 C)
C) 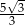 D) 5
D) 5
Znajdź wszystkie liczby całkowite spełniające nierówność 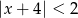 .
.
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 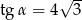 oblicz wartość wyrażenia
oblicz wartość wyrażenia 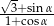 .
.
Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.
W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm. Oblicz pole tego trójkąta.
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia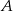 – na każdej kostce wypadła nieparzysta liczba oczek,
– na każdej kostce wypadła nieparzysta liczba oczek,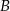 – suma wyrzuconych oczek jest nie mniejsza niż 8.
– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 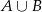 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 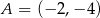 oraz
oraz 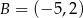 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 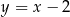 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Pierwiastkami wielomianu 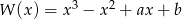 są tylko dwie liczby: 2 oraz (-3).
są tylko dwie liczby: 2 oraz (-3).
- Oblicz
 i
i 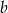 .
. - Zapisz wielomian w postaci czynników liniowych.
Z miejscowości 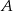 i
i 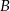 , które są odległe o 58,5 km wyruszyły jednocześnie ku sobie dwa samochody. Pierwszy samochód w ciągu pierwszej minuty jechał ze średnią prędkością 30 km/h, a w ciągu każdej następnej minuty pokonywał drogę o 0,25 km dłuższą, niż w ciągu poprzedniej minuty. Drugi samochód przez pierwsze 6 minut przejechał 21 kilometrów, a potem jechał ze stałą prędkością 150 km/h. Oblicz po ilu minutach nastąpi spotkanie samochodów.
, które są odległe o 58,5 km wyruszyły jednocześnie ku sobie dwa samochody. Pierwszy samochód w ciągu pierwszej minuty jechał ze średnią prędkością 30 km/h, a w ciągu każdej następnej minuty pokonywał drogę o 0,25 km dłuższą, niż w ciągu poprzedniej minuty. Drugi samochód przez pierwsze 6 minut przejechał 21 kilometrów, a potem jechał ze stałą prędkością 150 km/h. Oblicz po ilu minutach nastąpi spotkanie samochodów.

