Zestaw użytkownika nr 9982_2411
Zestaw użytkownika
nr 9982_2411
Funkcja 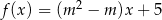 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 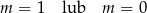 B)
B) 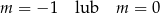 C)
C) 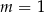 D)
D) 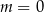
Mniejszą z dwóch liczb spełniających równanie 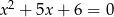 jest
jest
A) -1 B) -6 C) -2 D) -3
Osią symetrii paraboli będącej wykresem funkcji 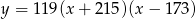 jest prosta o równaniu
jest prosta o równaniu
A) 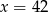 B)
B) 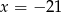 C)
C) 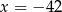 D)
D) 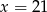
Wierzchołek paraboli będącej wykresem funkcji 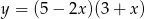 ma współrzędne
ma współrzędne
A) 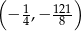 B)
B) 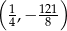 C)
C) 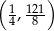 D)
D) 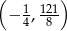
Wyznacz współczynniki  i
i 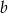 funkcji kwadratowej
funkcji kwadratowej 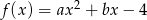 , jeśli współrzędne wierzchołka wynoszą
, jeśli współrzędne wierzchołka wynoszą 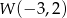 . Przedstaw trójmian w postaci iloczynowej.
. Przedstaw trójmian w postaci iloczynowej.
Zbiorem wartości funkcji kwadratowej 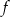 jest przedział
jest przedział 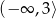 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 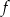 ?
?
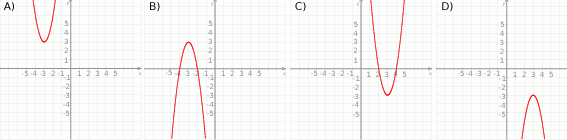
Zbiorem rozwiązań nierówności 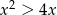 jest
jest
A) 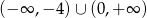 B)
B) 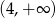 C)
C) 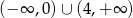 D)
D) 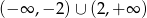
Liczba punktów wspólnych wykresu funkcji 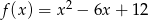 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 2 B) 3 C) 0 D) 1
Wyznacz najmniejszą i największą wartość funkcji 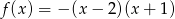 w przedziale
w przedziale 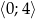 .
.
Dana jest funkcja 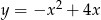 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor
. Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor ![→ u = [− 2,3]](https://img.zadania.info/zad/9470655/HzadT1x.gif) . Narysuj oba wykresy.
. Narysuj oba wykresy.
Funkcja kwadratowa określona wzorem 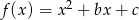 osiąga wartości ujemne wtedy i tylko wtedy, gdy
osiąga wartości ujemne wtedy i tylko wtedy, gdy 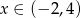 .
.
- Wyznacz wartości współczynników
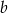 i
i  .
. - Oblicz, dla jakich argumentów
 , wartości funkcji
, wartości funkcji 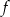 są mniejsze od wartości funkcji kwadratowej
są mniejsze od wartości funkcji kwadratowej 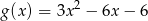 .
. - Rozwiąż równanie
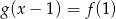 .
.

