/Szkoła średnia

Zadanie nr 1001018

Dodaj do ulubionych
Dodaj do rozwiązanych

W urnie znajdują się jedynie kule białe i czarne. Kul białych jest trzy razy więcej niż czarnych. Oblicz, ile jest kul w urnie, jeśli przy jednoczesnym losowaniu dwóch kul prawdopodobieństwo otrzymania kul o różnych kolorach jest większe od 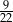-9 22 .

Rozwiązanie

Oznaczmy liczbę kul czarnych przez 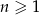n ≥ 1 . W takim razie jest 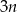3n kul białych. Za zdarzenia elementarne przyjmujemy dwuelementowe zbiory wylosowanych kul, czyli

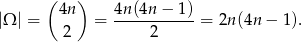
( ) 4n 4n-(4n−--1) |Ω | = 2 = 2 = 2n (4n − 1).

Zdarzenia sprzyjające to takie, w których mamy jedną kulę białą i jedną czarną, jest więc ich (zasada mnożenia))

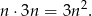
2 n⋅ 3n = 3n .

Pozostało rozwiązać nierówność

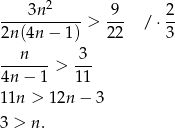
3n2 9 2 ----------- > --- / ⋅ -- 2n (4n− 1) 22 3 ---n---> -3- 4n − 1 11 11n > 12n − 3 3 > n .

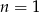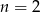Zatem n = 1 lub n = 2 i w urnie jest 4 lub 8 kul.  
Odpowiedź: 4 lub 8

Wersja PDF