Zadanie nr 1004692
Dla jakich wartości parametru 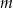 równanie
równanie 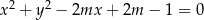 opisuje okrąg?
opisuje okrąg?
- Podaj współrzędne środka i długość promienia okręgu.
- Dla jakich wartości parametru
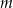 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 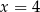 ?
?
Rozwiązanie
Przekształcamy podane równanie (zwijamy do pełnych kwadratów)
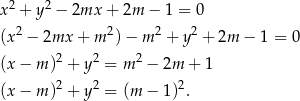
Otrzymane równanie jest równaniem okręgu wtedy i tylko wtedy gdy prawa strona jest dodatnia (bo ma to być kwadrat promienia), czyli dla 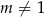 .
.
- Środek i promień okręgu to odpowiednio
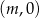 i
i 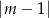 . Ta wartość bezwzględna przy promieniu jest bardzo ważna! – inczej mielibyśmy ujemny promień.
. Ta wartość bezwzględna przy promieniu jest bardzo ważna! – inczej mielibyśmy ujemny promień.
Odpowiedź: Środek: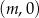 , promień:
, promień: 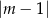
-
Sposób I
Okrąg jest styczny do prostej dokładnie wtedy gdy jego środek jest od tej prostej odległy o długość promienia. Moglibyśmy korzystać ze wzoru na odległość punktu od prostej, ale sytuacja jest na tyle banalna (prosta jest pionowa), że wystarczy zdrowy rozsądek. Odległość punktu
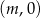 od prostej
od prostej 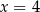 to dokładnie
to dokładnie 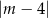 . Jak już stwierdziliśmy, odległość ta ma być równa promieniowi, co daje równanie
. Jak już stwierdziliśmy, odległość ta ma być równa promieniowi, co daje równanie 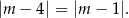
Wartości bezwzględne dwóch liczb są równe, gdy te liczby są równe, lub gdy są przeciwne. Mamy zatem dwa przypadki
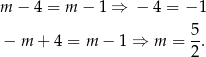
Na zakończenie możemy naszkicować sobie całą sytuację.
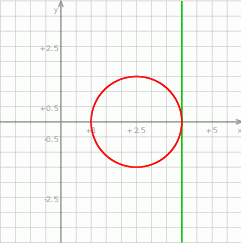
Sposób II
Możemy też skorzystać z faktu, że okrąg i prosta są styczne wtedy i tylko wtedy gdy mają jeden punkt wspólny. Zatem po wstawieniu do równania okręgu
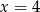 musimy otrzymać równanie, które ma dokładnie jedno rozwiązanie. Wstawiamy
musimy otrzymać równanie, które ma dokładnie jedno rozwiązanie. Wstawiamy 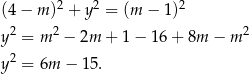
Jest tylko jedna możliwość, aby to równanie miało dokładnie jedno rozwiązanie: prawa strona musi być równa zero. Zatem
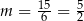 .
.
Odpowiedź: