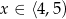/Szkoła średnia

Zadanie nr 1005377

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 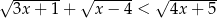√ ------- √ ------ √ ------- 3x + 1 + x − 4 < 4x + 5 .

Rozwiązanie

Ustalmy najpierw jaka jest dziedzina nierówności.

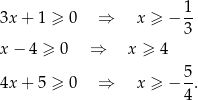
1 3x + 1 ≥ 0 ⇒ x ≥ − -- 3 x − 4 ≥ 0 ⇒ x ≥ 4 5 4x + 5 ≥ 0 ⇒ x ≥ − -. 4

Zatem musi być 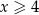x ≥ 4 . Lewa strona jest dodatnia, możemy więc nierówność podnieść stronami do kwadratu.

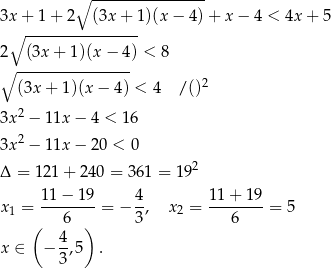
∘ ---------------- 3x + 1 + 2 (3x + 1)(x − 4) + x − 4 < 4x + 5 ∘ ---------------- 2 (3x+ 1)(x − 4) < 8 ∘ ---------------- (3x + 1)(x− 4) < 4 /()2 3x 2 − 11x − 4 < 16 2 3x − 11x − 20 < 0 Δ = 121 + 240 = 361 = 1 92 x = 11−--19-= − 4, x = 11-+-19-= 5 1 ( 6 ) 3 2 6 4 x ∈ − --,5 . 3

Uwzględniając dziedzinę nierówności, mamy 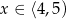x ∈ ⟨4,5) .  
Odpowiedź: x ∈ ⟨4,5 )

Wersja PDF