/Szkoła średnia

Zadanie nr 1006475

Dodaj do ulubionych
Dodaj do rozwiązanych

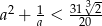Wykaż, że istnieje liczba dodatnia a , dla której 2 1 313√2- a + a < 20 .

Rozwiązanie

Aby ustalić możliwe wartości lewej strony nierówności, badamy funkcję 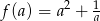f (a) = a2 + 1a określoną dla 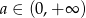a ∈ (0,+ ∞ ) . Liczymy pochodną.

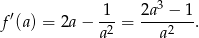
3 f ′(a) = 2a− 1--= 2a-−--1. a2 a2

Miejscem zerowym pochodnej jest 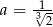a = 13√2- i pochodna przechodząc przez ten punkt zmienia znak z ujemnego na dodatni. W takim razie funkcja 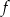f maleje w przedziale 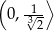( ⟩ 0, 13√2- i rośnie w przedziale 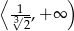⟨ ) -13√2,+ ∞ . To oznacza, że w punkcie 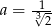-1- a = 3√2 funkcja 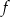f przyjmuje najmniejszą wartość. Obliczmy tę wartość

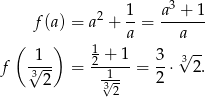
3 f (a) = a2 + 1-= a-+--1 a a ( 1 ) 1 + 1 3 √ -- f 3√--- = 2-----= --⋅ 32. 2 -13√2 2

Wystarczy teraz uzasadnić, że

√ -- 3 √3-- 31 3 2 20 --⋅ 2 < ------ / ⋅-3√--- 2 20 2 30 < 31.
Wersja PDF