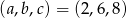/Szkoła średnia

Zadanie nr 1163465

Dodaj do ulubionych
Dodaj do rozwiązanych

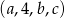Ciąg (a,4,b,c) jest arytmetyczny, a ciąg 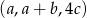(a,a+ b,4c) jest geometryczny. Oblicz 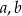a,b i c .

Rozwiązanie

Jeżeli ciąg 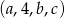(a,4,b,c) jest arytmetyczny, to

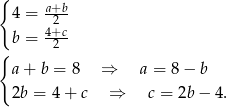
{ a+b- 4 = 2 b = 4+c2- { a+ b = 8 ⇒ a = 8− b 2b = 4 + c ⇒ c = 2b− 4.

Korzystamy teraz z informacji o tym, że ciąg 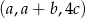(a,a + b,4c) jest geometryczny.

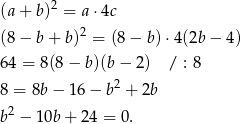
2 (a + b) = a⋅4c (8 − b + b)2 = (8− b )⋅4(2b − 4) 6 4 = 8(8 − b)(b − 2) / : 8 8 = 8b− 16 − b2 + 2b b 2 − 10b + 24 = 0.

Rozwiązujemy otrzymane równanie kwadratowe.

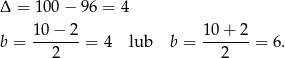
Δ = 10 0− 9 6 = 4 10 − 2 10 + 2 b = -------= 4 lub b = -------= 6. 2 2

Mamy wtedy odpowiednio

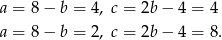
a = 8 − b = 4, c = 2b − 4 = 4 a = 8 − b = 2, c = 2b − 4 = 8 .

 
Odpowiedź: 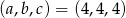(a,b,c) = (4 ,4,4) lub (a,b,c) = (2 ,6,8)

Wersja PDF