/Szkoła średnia

Zadanie nr 1272615

Dodaj do ulubionych
Dodaj do rozwiązanych

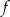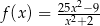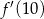Dana jest funkcja f określona wzorem 25x2−9- f(x) = x2+ 2 dla każdej liczby rzeczywistej x . Oblicz wartość f′(10) pochodnej tej funkcji dla argumentu 10.

Rozwiązanie

Korzystamy ze wzoru na pochodną ilorazu

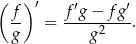
( ) ′ ′ ′ f- = f-g−--fg-. g g2

Sposób I

Liczymy

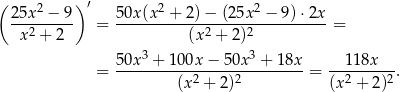
( 25x 2 − 9 ) ′ 50x(x2 + 2) − (25x 2 − 9) ⋅2x --------- = -----------------------------= x 2 + 2 (x 2 + 2 )2 50x3 + 100x − 5 0x3 + 18x 118x = ----------2-----2---------= --2-----2. (x + 2) (x + 2)

Mamy zatem

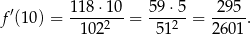
11 8⋅10 59 ⋅5 2 95 f′(10) = -----2--= ---2--= -----. 102 51 2601

Sposób II

Zauważmy najpierw, że

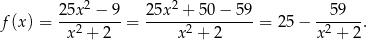
25x2 − 9 25x2 + 50 − 59 59 f(x) = --2------= -----2---------= 25 − -2-----. x + 2 x + 2 x + 2

W takim razie

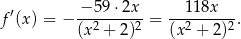
′ − 59 ⋅2x 118x f (x ) = − --2-----2-= --2-----2. (x + 2) (x + 2)

Pochodną w punkcie 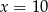x = 10 obliczamy tak samo jak poprzednio.  
Odpowiedź: f′(10) = 2296051-

Wersja PDF