Zadanie nr 1371849
Dany jest ciąg geometryczny 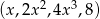 o wyrazach nieujemnych. Wtedy
o wyrazach nieujemnych. Wtedy
A) 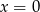 B)
B) 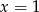 C)
C) 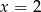 D)
D) 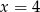
Rozwiązanie
Sposób I
W ciągu geometrycznym kwadrat każdego wyrazu (z wyjątkiem pierwszego i ostatniego) jest iloczynem wyrazów sąsiednich. Mamy więc
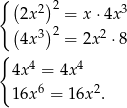
Z drugiego równania mamy
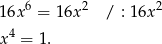
Ponieważ wyrazy ciągu są dodatnie mamy stąd 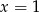 .
.
Sposób II
Ponieważ 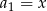 i
i 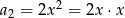 iloraz ciągu jest równy
iloraz ciągu jest równy 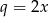 . Mamy stąd
. Mamy stąd
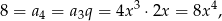
czyli 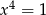 . Ponieważ wyrazy ciągu są dodatnie mamy stąd
. Ponieważ wyrazy ciągu są dodatnie mamy stąd 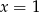 .
.
Odpowiedź: B

