Zadanie nr 1432652
W pewnej loterii fantowej przygotowano dwie urny z losami, przy czym w drugiej urnie było trzy razy więcej losów niż w pierwszej urnie. Prawdopodobieństwo wybrania losu wygrywającego z pierwszej urny jest równe  , a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe
, a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe 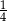 . Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
. Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
A) 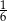 B)
B) 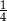 C)
C) 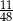 D)
D) 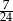
Rozwiązanie
Jeżeli w pierwszej urnie było  losów wygrywających, to wszystkich losów w pierwszej urnie było
losów wygrywających, to wszystkich losów w pierwszej urnie było 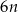 . W takim razie w drugiej urnie było
. W takim razie w drugiej urnie było 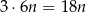 losów i wśród nich było
losów i wśród nich było 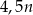 wygrywających. Po zmieszaniu losów z obu urn prawdopodobieństwo wygranej jest więc równe
wygrywających. Po zmieszaniu losów z obu urn prawdopodobieństwo wygranej jest więc równe
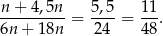
Odpowiedź: C

