Zadanie nr 1482944
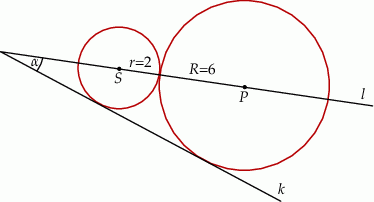
Dwa okręgi o promieniach 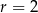 i
i 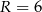 są styczne zewnętrznie i są styczne do wspólnej prostej
są styczne zewnętrznie i są styczne do wspólnej prostej  . Wykaż, że prosta
. Wykaż, że prosta  przechodząca przez środki
przechodząca przez środki 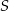 i
i 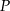 tych okręgów przecina prostą
tych okręgów przecina prostą 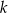 pod kątem
pod kątem 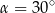 (zobacz rysunek).
(zobacz rysunek).
Rozwiązanie
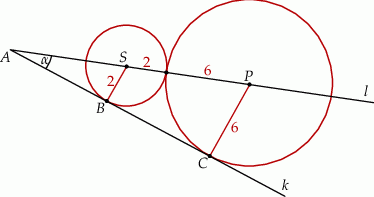
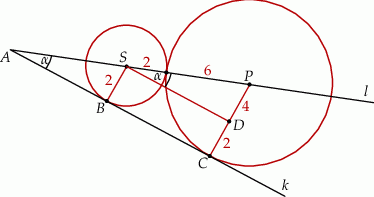
Niech 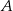 będzie punktem wspólnym prostych
będzie punktem wspólnym prostych 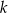 i
i 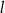 oraz oznaczmy punkty styczności okręgów z prostą
oraz oznaczmy punkty styczności okręgów z prostą  przez
przez  i
i  .
.
Sposób I
Trójkąty 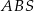 i
i 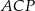 są podobne, więc
są podobne, więc
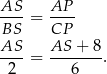
Stąd
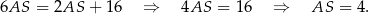
Mamy zatem
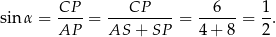
To oznacza, że 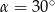 .
.
Sposób II
Niech 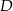 będzie rzutem punktu
będzie rzutem punktu 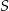 na promień
na promień 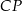 .
.
Czworokąt 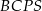 jest prostokątem, więc
jest prostokątem, więc
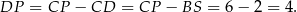
Ponadto 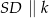 , więc
, więc
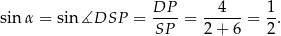
To oznacza, że 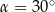 .
.

