Zadanie nr 1523324
Dany jest stożek o objętości 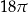 , którego przekrojem osiowym jest trójkąt
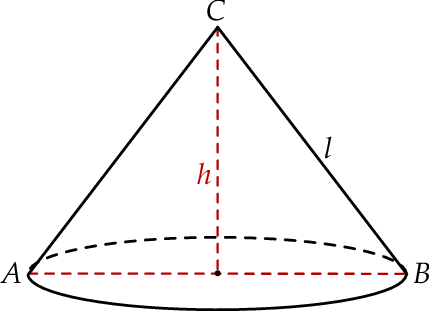
, którego przekrojem osiowym jest trójkąt 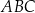 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 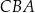 jest kątem nachylenia tworzącej
jest kątem nachylenia tworzącej 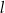 tego stożka do płaszczyzny jego podstawy. Tangens kąta
tego stożka do płaszczyzny jego podstawy. Tangens kąta 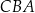 jest równy 2.
jest równy 2.
Wynika stąd, że wysokość 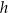 tego stożka jest równa
tego stożka jest równa
A) 12 B) 6 C) 4 D) 2
Rozwiązanie
Oznaczmy przez  promień podstawy stożka.
promień podstawy stożka.
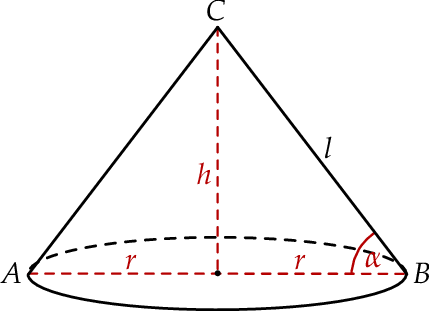
Z podanego tangensa mamy
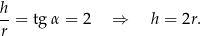
Korzystamy teraz z podanej objętości stożka.
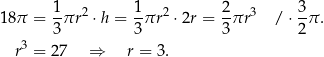
Wysokość stożka ma więc długość 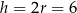 .
.
Odpowiedź: B

