/Szkoła średnia

Zadanie nr 1525726

Dodaj do ulubionych
Dodaj do rozwiązanych

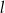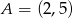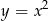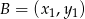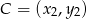Prosta l , na której leży punkt A = (2,5) , przecina parabolę o równaniu y = x2 w dwóch różnych punktach B = (x1,y1) i C = (x2,y2) . Oblicz wartość współczynnika kierunkowego prostej 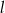l , przy której suma 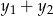y1 + y2 osiągnie wartość najmniejszą.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

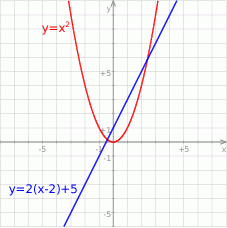
Proste przechodzące przez punkt 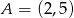A = (2,5) mają postać

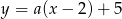
y = a(x − 2) + 5

(tak naprawdę brakuje w tym pęku pionowej prostej 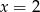x = 2 , ale ona przecina parabolę tylko w jednym punkcie). Szukamy teraz punktów wspólnych tej prostej z daną parabolą.

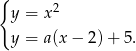
{ y = x2 y = a(x− 2)+ 5.

Porównujemy 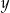y –ki.

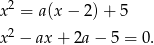
x 2 = a(x − 2)+ 5 2 x − ax + 2a− 5 = 0.

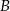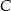Zauważmy teraz, że nie interesują nas dokładne wartości pierwiastków, ale ich suma kwadratów (bo punkty B i C leżą na paraboli).

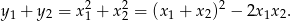
y1 + y2 = x 21 + x 22 = (x1 + x2)2 − 2x1x2.

Korzystamy teraz ze wzorów Viète’a.

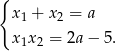
{ x1 + x2 = a x1x2 = 2a − 5.

Mamy zatem

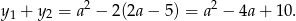
2 2 y1 + y2 = a − 2(2a − 5) = a − 4a + 10 .

Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość przyjmuje w wierzchołku, czyli dla 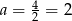a = 42 = 2 . Sprawdźmy jeszcze, że dla takiej wartości a prosta rzeczywiście przecina parabolę w dwóch punktach (czyli, że mogliśmy zastosować wzory Viète’a). Liczymy Δ -ę otrzymanego wyżej równania kwadratowego

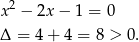
x 2 − 2x − 1 = 0 Δ = 4 + 4 = 8 > 0.

 
Odpowiedź: 2

Wersja PDF