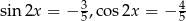/Szkoła średnia

Zadanie nr 1565565

Dodaj do ulubionych
Dodaj do rozwiązanych

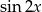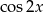Wyznacz sin 2x i cos2x jeśli wiadomo, że 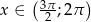(3π- ) x ∈ 2 ;2π i tg x = − 3 .

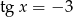Rozwiązanie

Sposób I

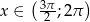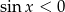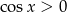Skoro ( 3π- ) x ∈ 2 ;2π (IV ćwiartka), to wiemy, że sin x < 0 i cos x > 0 . Liczymy więc

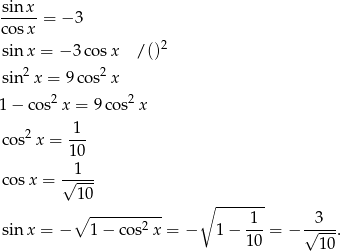
sinx ----- = − 3 cosx sinx = − 3cos x / ()2 2 2 sin x = 9cos x 1− cos2x = 9cos2 x cos2 x = -1- 10 1 cos x = √---- 10 ∘ ------- ∘ ---------- 1 3 sinx = − 1 − cos2 x = − 1 − 1-0 = − √----. 10

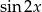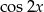Możemy teraz obliczyć sin 2x i co s2x .

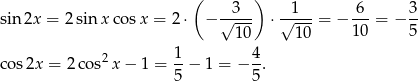
( 3 ) 1 6 3 sin 2x = 2 sinx cos x = 2 ⋅ − √---- ⋅ √----= − ---= − -- 10 10 10 5 2 1- 4- c os2x = 2cos x− 1 = 5 − 1 = − 5.

Sposób II

Jeżeli ktoś ma akurat pod ręką tablice matematyczne, to może tam znaleźć wzorki

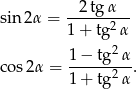
sin 2α = --2tg-α-- 1 + tg2α 2 cos2 α = 1-−-tg-α-. 1 + tg2α

Z tych wzorków mamy od razu rozwiązanie

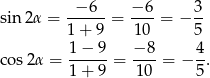
sin 2α = -−-6--= −-6-= − 3- 1 + 9 10 5 1 − 9 − 8 4 cos2 α = ------= ----= − -. 1 + 9 10 5

 
Odpowiedź: 3 4 sin 2x = − 5,cos2x = − 5

Wersja PDF