Zadanie nr 1828886
W skarbcu królewskim było 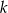 monet. Pierwszego dnia rano skarbnik dorzucił 25 monet, a każdego następnego ranka dorzucał o 2 monety więcej niż dnia poprzedniego. Jednocześnie ze skarbca król zabierał w południe każdego dnia 50 monet. Oblicz najmniejszą liczbę
monet. Pierwszego dnia rano skarbnik dorzucił 25 monet, a każdego następnego ranka dorzucał o 2 monety więcej niż dnia poprzedniego. Jednocześnie ze skarbca król zabierał w południe każdego dnia 50 monet. Oblicz najmniejszą liczbę 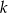 , dla której w każdym dniu w skarbcu była co najmniej jedna moneta, a następnie dla tej wartości
, dla której w każdym dniu w skarbcu była co najmniej jedna moneta, a następnie dla tej wartości 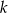 oblicz, w którym dniu w skarbcu była najmniejsza liczba monet.
oblicz, w którym dniu w skarbcu była najmniejsza liczba monet.
Rozwiązanie
Zastanówmy się jak zmienia się liczba monet w skarbcu każdego dnia. Skarbnik dorzuca 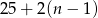 monet, gdzie
monet, gdzie  oznacza numer kolejnego dnia, a król zabiera 50. W sumie liczba monet zmienia się więc o
oznacza numer kolejnego dnia, a król zabiera 50. W sumie liczba monet zmienia się więc o
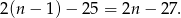
Zatem jeżeli przez 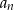 oznaczymy liczbę monet w skarbcu po południu
oznaczymy liczbę monet w skarbcu po południu  -tego dnia (jak już król zabierze swoją dolę :)), to mamy
-tego dnia (jak już król zabierze swoją dolę :)), to mamy
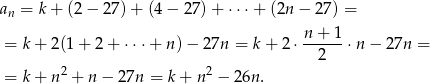
Pytanie teraz brzmi, dla jakiej najmniejszej wartości 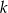 , wyrażenie to jest dodatnie dla dowolnego
, wyrażenie to jest dodatnie dla dowolnego 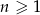 . Wykresem funkcji
. Wykresem funkcji 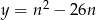 jest parabola o ramionach skierowanych w górę, więc najmniejsza wartość przyjmuje w wierzchołku
jest parabola o ramionach skierowanych w górę, więc najmniejsza wartość przyjmuje w wierzchołku
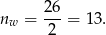
Wartość ta jest równa
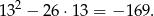
Zatem 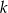 musi być co najmniej równe 170.
musi być co najmniej równe 170.
Odpowiedź: 13 dnia,