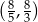/Szkoła średnia

Zadanie nr 1833395

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 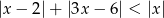|x − 2|+ |3x − 6| < |x | .

Rozwiązanie

Sposób I

Aby opuścić wartości bezwzględne, musimy wiedzieć jaki jest znak zawartych w nich wyrażeń. Pierwsze dwa są ujemne dla 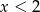x < 2 a trzecie dla 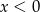x < 0 . Zatem dana nierówność prowadzi do nierówności

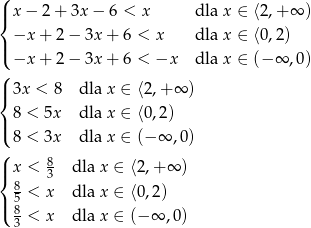
( |{ x− 2+ 3x − 6 < x dla x ∈ ⟨2 ,+ ∞ ) | −x + 2− 3x+ 6 < x dla x ∈ ⟨0 ,2) ( −x + 2− 3x+ 6 < −x dla x ∈ (− ∞ ,0 ) ( |{ 3x < 8 dla x ∈ ⟨2,+ ∞ ) 8 < 5x dla x ∈ ⟨0,2) |( 8 < 3x dla x ∈ (− ∞ ,0 ) ( 8 |{ x < 3 dla x ∈ ⟨2,+ ∞ ) 85 < x dla x ∈ ⟨0,2) |( 8 < x dla x ∈ (− ∞ ,0) 3

Rozwiązaniem tych nierówności jest zbiór

( 8 8 ) -,-- . 5 3

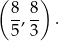
Sposób II

Ponieważ

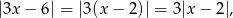
|3x− 6| = |3(x− 2)| = 3|x− 2|,

to podaną nierówność możemy zapisać w postaci

4|x− 2| < |x|.

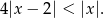
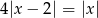Geometrycznie, nierówność ta oznacza, że odległość x od 0 ma być większa niż 4 odległości od 2. Punkty, w których 4 |x − 2 | = |x| to rozwiązania równań

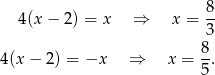
4(x − 2) = x ⇒ x = 8- 3 8 4(x − 2 ) = −x ⇒ x = -. 5

Jeżeli zaznaczymy te punkty na osi, to można zauważyć, że 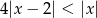4|x − 2| < |x| w przedziale 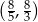(8 8) 5,3 (na zewnątrz tego przedziału odległość x od 0 robi się mniejsza niż 4|x − 2| ).

PIC

 
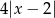Odpowiedź: ( ) 85, 83

Wersja PDF