/Szkoła średnia

Zadanie nr 2273603

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są dwa zbiory:

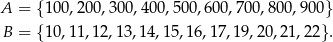
A = {10 0,200,300,4 00,500,600 ,700,800,90 0} B = {10 ,1 1,12,13,14,1 5,16,17,19,2 0,21,22}.

Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 9.

Rozwiązanie

Liczbę z pierwszego zbioru możemy wybrać na 9 sposobów, a liczbę z drugiego zbioru na 12 sposobów. Jest więc

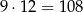
9 ⋅12 = 10 8

zdarzeń elementarnych. Łatwo wypisać wszystkie zdarzenia sprzyjające (suma cyfr otrzymanej liczby musi się dzielić przez 9):

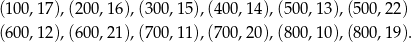
(1 00,17),(200,16 ),(300,15),(400 ,14),(500,13),(50 0,22) (6 00,12),(600,21 ),(700,11),(700 ,20),(800,10),(80 0,19).

Jest tych zdarzeń 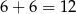6 + 6 = 12 , więc interesujące nas prawdopodobieństwo jest równe

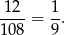
12 1 ----= -. 108 9

 
Odpowiedź: 1 9

Wersja PDF