Jeżeli wymnożymy lewą stronę równości
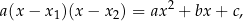
to otrzymamy tak zwane wzory Viète’a dla równania kwadratowego.
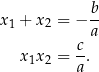
Inny prosty sposób wyprowadzenia tych wzorów to użycie wzorów na pierwiastki równania kwadratowego.
Cały urok wzorów Viète’a polega na tym, że są bardzo proste – na przykład nie ma w nich pierwiastków. W wielu sytuacjach same rozwiązania równania mogą być dość paskudne, natomiast wzory Viète’a dają bardzo proste wyrażenia na 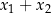 i
i 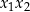 .
.
Równanie
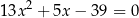
ma dość skomplikowane rozwiązania, ale nie trzeba ich liczyć, żeby stwierdzić, że ich iloczyn jest równy 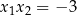 , a suma
, a suma 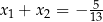 . Co to daje? – na przykład widać z tego, że pierwiastki są różnych znaków (iloczyn jest ujemny) – jest to bardzo popularne zastosowanie wzorów Viète’a.
. Co to daje? – na przykład widać z tego, że pierwiastki są różnych znaków (iloczyn jest ujemny) – jest to bardzo popularne zastosowanie wzorów Viète’a.
Równanie musi mieć pierwiastki! Niezwykle ważne jest pamiętanie o tym, że dopóki zajmujemy się tylko liczbami rzeczywistymi, to wzory Viète’a mają sens tylko wtedy, gdy równanie ma pierwiastki, to znaczy gdy 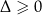 .
.
Możemy sobie napisać wzorki 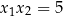 ,
, 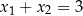 dla równania
dla równania 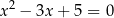 , ale dopóki nie nauczymy się liczb zespolonych, wzory te nie mają sensu, bo to równanie nie ma pierwiastków rzeczywistych.
, ale dopóki nie nauczymy się liczb zespolonych, wzory te nie mają sensu, bo to równanie nie ma pierwiastków rzeczywistych.
Uwaga ta jest szczególnie ważna w zadaniach z parametrem – zanim zaczniemy pisać wzory Viète’a musimy sprawdzić, kiedy równanie ma rozwiązania.
Dla jakiej wartości 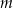 suma różnych pierwiastków równania
suma różnych pierwiastków równania
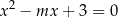
jest większa od 1? Jeżeli równanie ma pierwiastki, to na mocy wzorów Viète’a, tak będzie, gdy 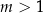 . Aby sprawdzić kiedy istnieją pierwiastki, musimy dodatkowo rozwiązać nierówność
. Aby sprawdzić kiedy istnieją pierwiastki, musimy dodatkowo rozwiązać nierówność 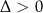 . Ostateczną odpowiedzią jest
. Ostateczną odpowiedzią jest 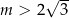 .
.
Cała potęga wzorów Viète’a ujawnia się w przypadku równań z parametrem. Dla takich równań wzory na pierwiastki równania dają wyjątkowo brzydkie wyrażenia, a wzory Viète’a wręcz przeciwnie. Typowe dwa rodzaje zadań tego typu to ustalenie znaków pierwiastków oraz zadania z różnymi wyrażeniami typu 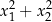 . Omówimy teraz krótko obie sytuacje. Znaki pierwiastków Jak już wiemy, wzory Viète’a dają nam informację o iloczynie
. Omówimy teraz krótko obie sytuacje. Znaki pierwiastków Jak już wiemy, wzory Viète’a dają nam informację o iloczynie 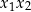 i sumie
i sumie 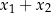 . Jak na tej podstawie ustalić jakie są znaki
. Jak na tej podstawie ustalić jakie są znaki 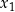 i
i 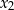 ?
?
| Znak iloczynu | Znaki pierwiastków |
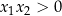 | Pierwiastki są tych samych znaków, oba dodatnie gdy 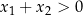 i ujemne gdy i ujemne gdy 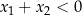 . . |
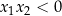 | Pierwiastki są różnych znaków. |
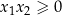 | Pierwiastki są tego samego znaku lub zerowe; nieujemne gdy 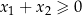 i niedodatnie gdy i niedodatnie gdy 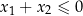 . . |
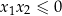 | Jeden pierwiastek jest niedodatni, a drugi nieujemny |
Oczywiście nie ma sensu uczyć się powyższych formułek na pamięć – trzeba po prostu pamiętać, że na podstawie znaków 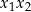 i
i 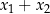 można ustalić znak
można ustalić znak 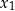 i
i 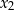 .
.
Kiedy pierwiastki równania 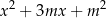 są ujemne?
są ujemne?
Łatwo sprawdzić, że równanie ma zawsze pierwiastki, możemy więc stosować wzory Viète’a. Jeżeli liczby są ujemne, to ich iloczyn musi być dodatni (czyli 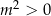 ). Czy wystarczy sprawdzić ten warunek? – nie, bo iloczyn dwóch liczb dodatnich też jest dodatni; musimy jeszcze sprawdzić czy suma jest ujemna (czyli
). Czy wystarczy sprawdzić ten warunek? – nie, bo iloczyn dwóch liczb dodatnich też jest dodatni; musimy jeszcze sprawdzić czy suma jest ujemna (czyli 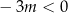 ) – w ten sposób wyeliminujemy tę drugą możliwość.
) – w ten sposób wyeliminujemy tę drugą możliwość.
Wyrażenia z pierwiastkami Jeden z popularnych motywów w zadaniach na wzory Viète’a jest oparty o fakt, że każde symetryczne wyrażenie od 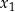 i
i 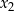 daje się przedstawić jako wyrażanie wielomianowe, w którym występują tylko
daje się przedstawić jako wyrażanie wielomianowe, w którym występują tylko 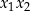 i
i 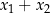 . Trochę to skomplikowanie brzmi, więc napiszmy kilka przykładów
. Trochę to skomplikowanie brzmi, więc napiszmy kilka przykładów
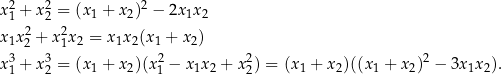
Na mocy wzorów Viète’a każde wyrażenie tego typu może być łatwo wyrażone od współczynników wielomianu. Tego typu przekształcenia działają zawsze, gdy wyrażenie jest symetryczne, to znaczy gdy nie zmienia się przy zamianie 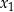 i
i 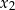 miejscami – wszystkie wypisane wyżej wyrażenia są symetryczne. Dla odmiany, wyrażenie
miejscami – wszystkie wypisane wyżej wyrażenia są symetryczne. Dla odmiany, wyrażenie  nie jest symetryczne i nie da się go wyrazić przez
nie jest symetryczne i nie da się go wyrazić przez 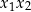 i
i 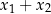 . (Natomiast
. (Natomiast 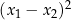 już jest symetryczne).
już jest symetryczne).
Oblicz sumę kwadratów pierwiastków równania
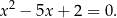
Liczymy
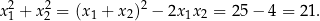
Układy równań Zacznijmy od przykładu.
Układ równań
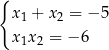
możemy rozwiązać następująco: na mocy wzorów Viète’a rozwiązania tego układu są pierwiastkami równania 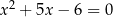 . Daje nam to dwie pary rozwiązań:
. Daje nam to dwie pary rozwiązań: 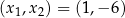 i
i 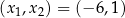 .
.
Powyższy sposób rozwiązania jest bardzo elegancki – gdybyśmy robili to tradycyjnie, czyli na przykład wyliczyli 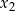 z drugiego równania i podstawili do pierwszego, to musimy dzielić przez
z drugiego równania i podstawili do pierwszego, to musimy dzielić przez 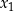 , a więc musimy osobno się zastanowić, co się dzieje, gdy
, a więc musimy osobno się zastanowić, co się dzieje, gdy 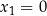 ; potem musimy jeszcze przekształcić pierwsze równanie, a na koniec i tak dostaniemy to samo równanie kwadratowe, które przed chwilą rozwiązaliśmy.
; potem musimy jeszcze przekształcić pierwsze równanie, a na koniec i tak dostaniemy to samo równanie kwadratowe, które przed chwilą rozwiązaliśmy.
Opisana metoda może być zastosowana do dowolnego układu równań z dwoma niewiadomymi 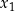 i
i 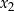 , w którym równania są symetryczne – podstawiamy
, w którym równania są symetryczne – podstawiamy 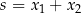 ,
, 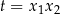 i rozwiązujemy układ (w jakikolwiek sposób), a na koniec wyliczamy
i rozwiązujemy układ (w jakikolwiek sposób), a na koniec wyliczamy 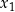 i
i 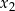 , tak jak to opisaliśmy wyżej.
, tak jak to opisaliśmy wyżej.
W układzie
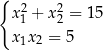
podstawiamy 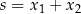 ,
, 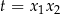 i mamy układ równań
i mamy układ równań
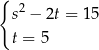
Łatwo z tego układu wyznaczyć 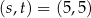 lub
lub 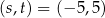 . Zatem
. Zatem 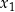 i
i 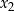 są pierwiastkami równania
są pierwiastkami równania 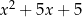 lub
lub 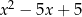 . Daje to nam 4 rozwiązania wyjściowego układu.
. Daje to nam 4 rozwiązania wyjściowego układu.
Tips & Tricks
1Jeżeli w zadaniu z parametrem przewidujemy, że wyjdzie nam tylko kilka wartości parametru, to zamiast sprawdzać na początku kiedy 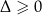 (lub
(lub 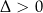 w zależności od polecenia), możemy na końcu sprawdzić otrzymane rozwiązania. Oczywiście ta metoda nic nie daje, gdy rozwiązaniem jest przedział lub gdy rozwiązań jest bardzo dużo.
w zależności od polecenia), możemy na końcu sprawdzić otrzymane rozwiązania. Oczywiście ta metoda nic nie daje, gdy rozwiązaniem jest przedział lub gdy rozwiązań jest bardzo dużo.
Kiedy suma pierwiastków równania
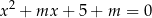
jest równa 3? Na mocy wzorów Viète’a będzie tak gdy 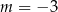 . Ponieważ wyszła nam tylko jedna wartość
. Ponieważ wyszła nam tylko jedna wartość 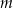 , to łatwiej jest sprawdzić, że dla
, to łatwiej jest sprawdzić, że dla 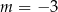 równanie ma pierwiastki, niż na początku rozwiązywać nierówność kwadratową
równanie ma pierwiastki, niż na początku rozwiązywać nierówność kwadratową 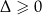 .
.
2Wzory Viète’a są niezwykle użyteczne przy sprawdzaniu czy dobrze rozwiązaliśmy równanie kwadratowe. Jeżeli chcemy mieć pewność, że się nie pomyliliśmy, to zamiast śledzić lub powtarzać rachunki, wystarczy otrzymane pierwiastki dodać i pomnożyć – jeżeli wyjdzie 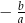 i
i  to pierwiastki są dobrze obliczone.
to pierwiastki są dobrze obliczone.
3Jeżeli znamy jeden pierwiastek równania kwadratowego, to ze wzoru 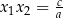 (lub ze wzoru
(lub ze wzoru 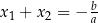 ) natychmiast mamy drugi.
) natychmiast mamy drugi.
Łatwo zobaczyć, że 1 jest pierwiastkiem równania
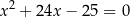
(przy odrobinie wprawy takie rzeczy widać od ręki – suma współczynników jest 0, więc 1 jest pierwiastkiem). W takim razie natychmiast wiemy, że -25 jest drugim pierwiastkiem (bo iloczyn rozwiązań jest równy -25).
Ten sam schemat pozwala łatwo zgadnąć rozwiązania prostych równań, w których pierwiastki są całkowite (bardzo częsta sytuacja w przypadku zadań szkolnych).
Jeżeli spodziewamy się, że równanie
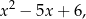
ma mieć całkowity pierwiastek, to musi to być dzielnik 6, czyli musi to być 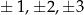 lub
lub 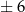 . W dodatku, iloczyn pierwiastków jest równy 6, zatem jeżeli 1 nie jest pierwiastkiem, to 6 też nie może być i tak dalej. W podanym przykładzie pierwiastki to 2 i 3.
. W dodatku, iloczyn pierwiastków jest równy 6, zatem jeżeli 1 nie jest pierwiastkiem, to 6 też nie może być i tak dalej. W podanym przykładzie pierwiastki to 2 i 3.
4 Wzory Viète’a można również stosować w sytuacjach, gdy podane wyrażenie z pierwiastkami nie jest symetryczne – zwykle daje nam to wtedy układ równań.
Dla jakich wartości parametru 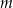 , różne pierwiastki równania
, różne pierwiastki równania 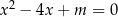 spełniają warunek
spełniają warunek 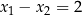 .
.
Deltę zostawiamy sobie na koniec. Na mocy wzorów Viète’a, mamy 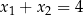 . Dodając tę równość do podanego warunku otrzymujemy
. Dodając tę równość do podanego warunku otrzymujemy 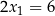 , czyli
, czyli 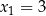 . Sprawdźmy teraz, kiedy
. Sprawdźmy teraz, kiedy 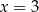 jest pierwiastkiem.
jest pierwiastkiem.

Z drugiego z wzorów Viète’a, wiemy że drugim pierwiastkiem równania
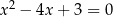
jest 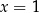 . Zatem równanie rzeczywiście ma dwa pierwiastki spełniające
. Zatem równanie rzeczywiście ma dwa pierwiastki spełniające 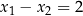 . Skoro znamy oba pierwiastki, to nie musimy już sprawdzać
. Skoro znamy oba pierwiastki, to nie musimy już sprawdzać 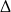 -y.
-y.
5Wzory Viète’a działają w przypadku 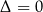 , o ile traktujemy ten jedyny w tym przypadku pierwiastek
, o ile traktujemy ten jedyny w tym przypadku pierwiastek 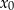 , jako dwa pierwiastki, które są równe, to znaczy
, jako dwa pierwiastki, które są równe, to znaczy
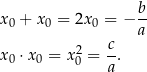
Powyższa obserwacja bywa źródłem wielu nieporozumień w szkolnych zadaniach ze wzorami Viète’a. Problem polega na braku jednoznacznej konwencji, czy równanie w przypadku 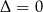 ma jeden pierwiastek, czy też ma dwa równe. Z punktu widzenia wzorów Viète’a (i jeszcze kilku innych) wygodnie jest przyjąć, że ma dwa pierwiastki – dzięki takiej umowie nie trzeba rozważać sytuacji
ma jeden pierwiastek, czy też ma dwa równe. Z punktu widzenia wzorów Viète’a (i jeszcze kilku innych) wygodnie jest przyjąć, że ma dwa pierwiastki – dzięki takiej umowie nie trzeba rozważać sytuacji 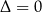 osobno.
osobno.
Dla jakich parametrów 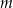 suma pierwiastków równania
suma pierwiastków równania 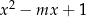 jest większa od 1?
jest większa od 1?
Typowe szkolne rozwiązanie, to sprawdzenie 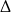 -y – daje to nam
-y – daje to nam 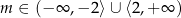 . Potem stosujemy wzory Viète’a
. Potem stosujemy wzory Viète’a
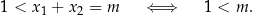
Czyli 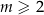 .
.
Czy to jest dobre rozwiązanie? – aby było, musimy założyć, że równanie
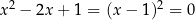
ma dwa pierwiastki równe 1. Jeżeli nie chcemy tego zakładać, to 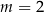 należy wyrzucić ze zbioru rozwiązań.
należy wyrzucić ze zbioru rozwiązań.
Powyższa wątpliwość na szczęście nie występuje, gdy zajmujemy się znakami pierwiastków.
Dla jakich parametrów 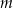 pierwiastki równania
pierwiastki równania 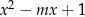 są dodatnie?
są dodatnie?
Jak poprzednio, z 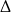 -y mamy
-y mamy 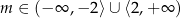 . Na mocy wzorów Viète’a mamy
. Na mocy wzorów Viète’a mamy
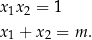
Widać więc, że pierwiastki będą dodatnie dla 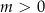 , co w połączeniu z ograniczeniem na
, co w połączeniu z ograniczeniem na 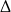 -ę, daje
-ę, daje 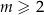 .
.
Tu nie ma problemu z przypadkiem 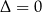 , bo znak pierwiastka nie zależy od tego, czy traktujemy go pojedynczo czy podwójnie.
, bo znak pierwiastka nie zależy od tego, czy traktujemy go pojedynczo czy podwójnie.
6Aby stosować podane wzory Viète’a musimy wiedzieć, że równanie jest kwadratowe – w przypadku równania z parametrem oznacza to konieczność osobnego rozpatrzenia przypadku, gdy współczynnik przy 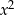 jest zerowy.
jest zerowy.
Dla jakich wartości parametru 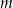 suma odwrotności pierwiastków równania
suma odwrotności pierwiastków równania 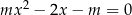 jest nieujemna?
jest nieujemna?
Łatwo sprawdzić, że 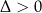 , więc na mocy wzorów Viète’a mamy
, więc na mocy wzorów Viète’a mamy
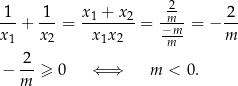
To jednak nie koniec, bo ten rachunek miał sens o ile 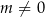 . Dla
. Dla 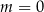 mamy równanie liniowe
mamy równanie liniowe 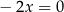 , więc też jest OK.
, więc też jest OK.
7W przypadku bardziej egzotycznych warunków ze znakami pierwiastków, warto się zastanowić, czy przypadkiem nie jest prościej ustalić, kiedy podany warunek nie jest spełniony.
Kiedy równanie
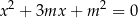
ma co najmniej jeden pierwiastek nieujemny? Sprawdzamy najpierw kiedy równanie ma w ogóle pierwiastki – okazuje się, że zawsze (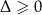 ). Kiedy jeden jest nieujemny? – trudno to zapisać przy pomocy znaków
). Kiedy jeden jest nieujemny? – trudno to zapisać przy pomocy znaków 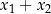 i
i 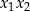 , za to bardzo łatwo jest zapisać warunek przeciwny, czyli że oba są ujemne. Musimy sprawdzić kiedy
, za to bardzo łatwo jest zapisać warunek przeciwny, czyli że oba są ujemne. Musimy sprawdzić kiedy
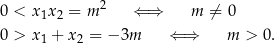
Zatem dla 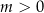 oba pierwiastki są ujemne, czyli dla
oba pierwiastki są ujemne, czyli dla 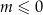 przynajmniej jeden jest nieujemny.
przynajmniej jeden jest nieujemny.
8Wprawdzie taka wiedza wykracza poza program szkolny, ale czasem warto sobie zdawać sprawę z faktu, że istnieją wzory Viète’a dla wielomianów dowolnego stopnia. Ich wyprowadzenie jest identyczne jak w przypadku równania kwadratowego.
Jeżeli wymnożymy lewą stronę równości
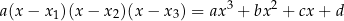
i porównamy współczynniki przy odpowiednich potęgach  , to otrzymamy wzory Viète’a dla wielomianu stopnia 3
, to otrzymamy wzory Viète’a dla wielomianu stopnia 3
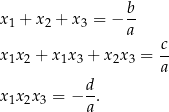
Pomimo, że wzory te są poza standardami szkolnymi, mogą być użyteczne w zadaniach typowo szkolnych.
Podobnie jak w przypadku równania kwadratowego, równość 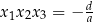 jest doskonałym sposobem na sprawdzenie, czy dobrze rozwiązaliśmy równanie stopnia 3.
jest doskonałym sposobem na sprawdzenie, czy dobrze rozwiązaliśmy równanie stopnia 3.
Rozwiążmy równanie 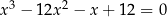 .
.
Dość łatwo jest zauważyć dwa pierwiastki tego równania (sprawdzając dzielniki wyrazu wolnego): 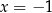 i
i 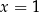 . Na mocy wzoru
. Na mocy wzoru 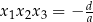 , trzecim pierwiastkiem jest
, trzecim pierwiastkiem jest 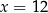 .
.
Rozwiążmy równanie 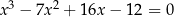 .
.
Sprawdzając dzielniki wyrazu wolnego znajdujemy pierwiastek 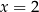 . Jeżeli napiszemy teraz pierwszy i trzeci wzór Viète’a przyjmując
. Jeżeli napiszemy teraz pierwszy i trzeci wzór Viète’a przyjmując 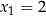 , to mamy
, to mamy
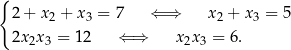
Zatem pozostałe pierwiastki równania są pierwiastkami równania kwadratowego
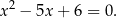
Rozwiązując to równanie dostajemy 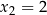 i
i 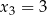 .
.

