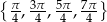/Szkoła średnia

Zadanie nr 2336626

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakiego 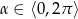α ∈ ⟨0,2 π⟩ pierwiastki równania

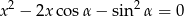
2 2 x − 2x cos α− sin α = 0

spełniają warunek 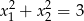2 2 x1 + x2 = 3 ?

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma pierwiastki.

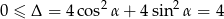
2 2 0 ≤ Δ = 4cos α + 4sin α = 4

Nierówność ta jest zawsze spełniona, więc równanie ma zawsze dwa pierwiastki 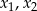x1,x 2 .

Na mocy wzorów Viète’a mamy

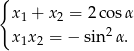
{ x 1 + x 2 = 2co sα 2 x 1x2 = − sin α.

Musimy rozwiązać równanie

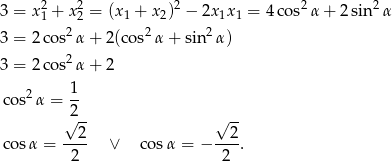
2 2 2 2 2 3 = x1 + x2 = (x1 + x2) − 2x1x1 = 4cos α+ 2sin α 3 = 2cos2 α+ 2(cos2α + sin2 α) 3 = 2cos2 α+ 2 1 cos2α = -- √2-- √ -- --2- --2- cosα = 2 ∨ co sα = − 2 .

Szkicujemy teraz cosinusa.

PIC

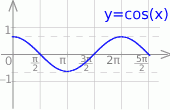
Z wykresu odczytujemy rozwiązania:

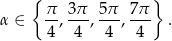
{ } α ∈ π-, 3-π , 5π-, 7π . 4 4 4 4

 
Odpowiedź: { } π-, 3π, 5π-, 7π 4 4 4 4

Wersja PDF