/Szkoła średnia

Zadanie nr 2536947

Dodaj do ulubionych
Dodaj do rozwiązanych

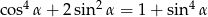Uzasadnij, że jeżeli α jest kątem ostrym, to 4 2 4 cos α+ 2sin α = 1 + sin α .

Rozwiązanie

Sposób I

Przekształcamy lewą stronę równości korzystając z jedynki trygonometrycznej.

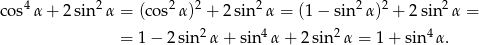
4 2 2 2 2 2 2 2 cos α+ 2sin α = (cos α) + 2sin α = (1− sin α) + 2 sin α = = 1 − 2 sin 2α + sin4α + 2 sin 2α = 1+ sin4 α.

Sposób II

Równość którą mamy udowodnić możemy zapisać w postaci

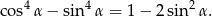
4 4 2 co s α − sin α = 1− 2sin α.

Przekształcamy lewą stronę korzystając ze wzoru na różnicę kwadratów oraz z jedynki trygonometrycznej.

4 4 2 2 2 2 L = cos α − sin α = (cos α) − (sin α) = = (co s2α − sin2α )(cos2α + sin2α ) = (cos2α − sin2 α) = 2 2 2 = (1 − sin α)− sin α = 1 − 2 sin α.
Wersja PDF