/Szkoła średnia

Zadanie nr 2689348

Dodaj do ulubionych
Dodaj do rozwiązanych

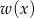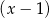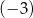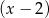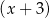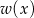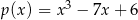Przy dzieleniu wielomianu w (x) przez dwumian (x − 1 ) otrzymujemy resztę (− 3) , przy dzieleniu przez dwumian (x − 2 ) resztę 6, a przy dzieleniu przez dwumian (x+ 3) resztę 1. Wyznacz resztę z dzielenia wielomianu w(x) przez wielomian p(x) = x 3 − 7x + 6 .

Rozwiązanie

Zauważmy najpierw, że

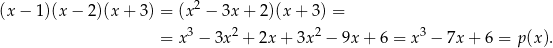
2 (x − 1)(x − 2)(x + 3) = (x − 3x + 2)(x+ 3) = = x 3 − 3x2 + 2x + 3x2 − 9x + 6 = x3 − 7x+ 6 = p(x ).

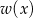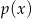Reszta z dzielenia wielomianu w (x) przez p(x) jest stopnia 2 (reszta ma zawsze stopień niższy, niż stopień wielomianu, przez który dzielimy), czyli

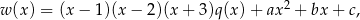
w (x) = (x − 1)(x − 2 )(x+ 3)q(x) + ax2 + bx + c,

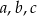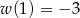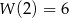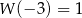dla pewnych a,b,c . Z podanych informacji wiemy, że w(1) = − 3 , W (2) = 6 i W (− 3) = 1 . Podstawiając te wartości w powyższej równości mamy

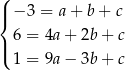
( |{ − 3 = a + b + c 6 = 4a + 2b + c |( 1 = 9a − 3b + c

Odejmujemy od drugiego równania pierwsze, a od ostatniego drugie, i dostajemy

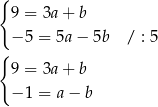
{ 9 = 3a + b − 5 = 5a − 5b / : 5 { 9 = 3a + b − 1 = a− b

Teraz dodajemy równania stronami i mamy

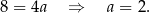
8 = 4a ⇒ a = 2.

Stąd 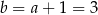b = a + 1 = 3 i

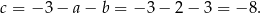
c = − 3 − a − b = − 3 − 2 − 3 = − 8.

Szukana reszta jest więc równa

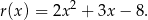
2 r(x) = 2x + 3x − 8 .

 
Odpowiedź: r(x) = 2x2 + 3x − 8

Wersja PDF