/Szkoła średnia

Funkcja kwadratowa

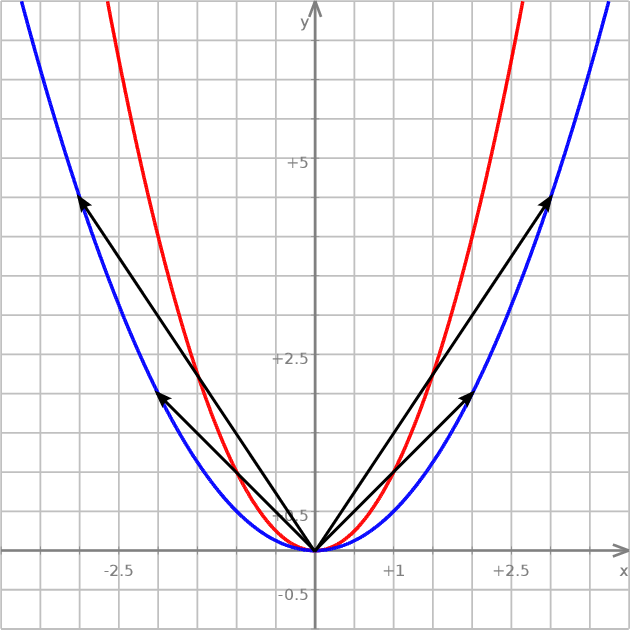
Wykresem funkcji kwadratowej

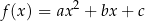
f(x ) = ax2 + bx + c

jest parabola. Jej ramiona są skierowane w górę gdy 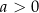a > 0 i w dół dla 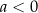a < 0 . Jeżeli 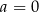a = 0 to funkcja jest liniowa. Parabola ma dwa rodzaje punktów szczególnych – wierzchołek i miejsca zerowe (punkty przecięcia z osią 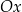Ox ). Miejsca zerowe to rozwiązania równania

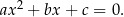
ax 2 + bx + c = 0.

  • Jeżeli równanie to ma dwa rozwiązania (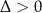Δ > 0 ) to są dwa miejsca zerowe.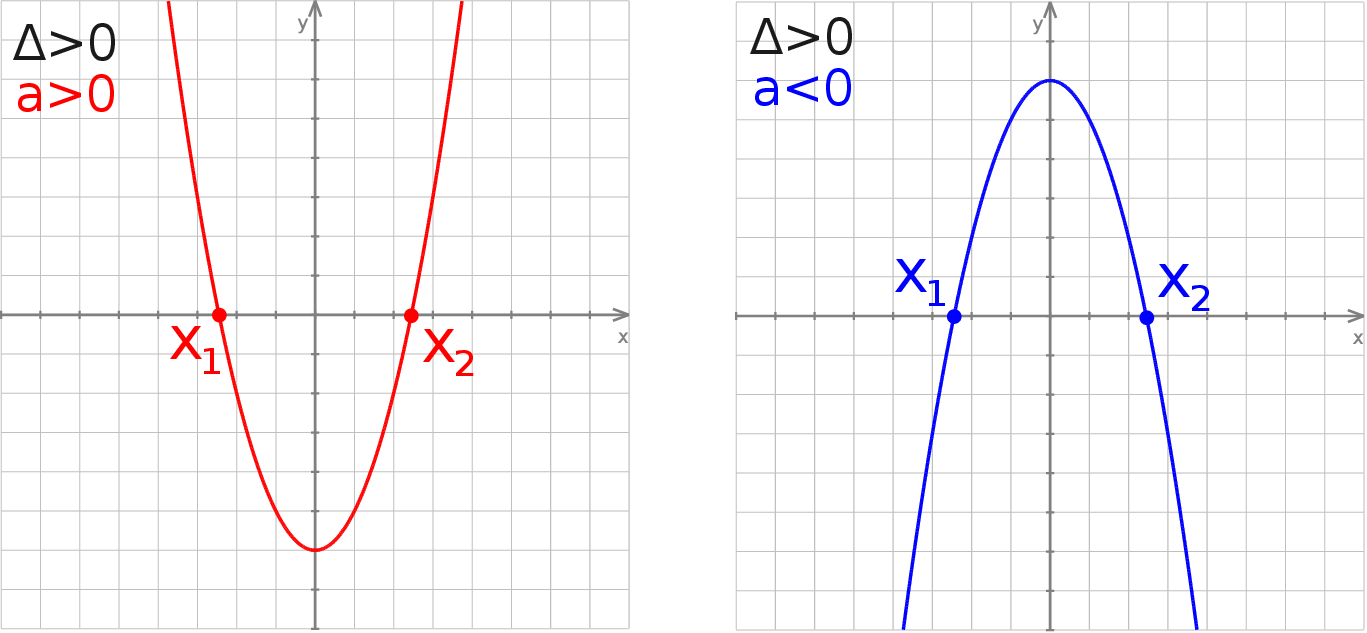

    ZINFO-FIGURE

  • Jeżeli jest tylko jedno miejsce zerowe (Δ = 0 ) to parabola jest styczna w wierzchołku do osi Ox

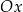
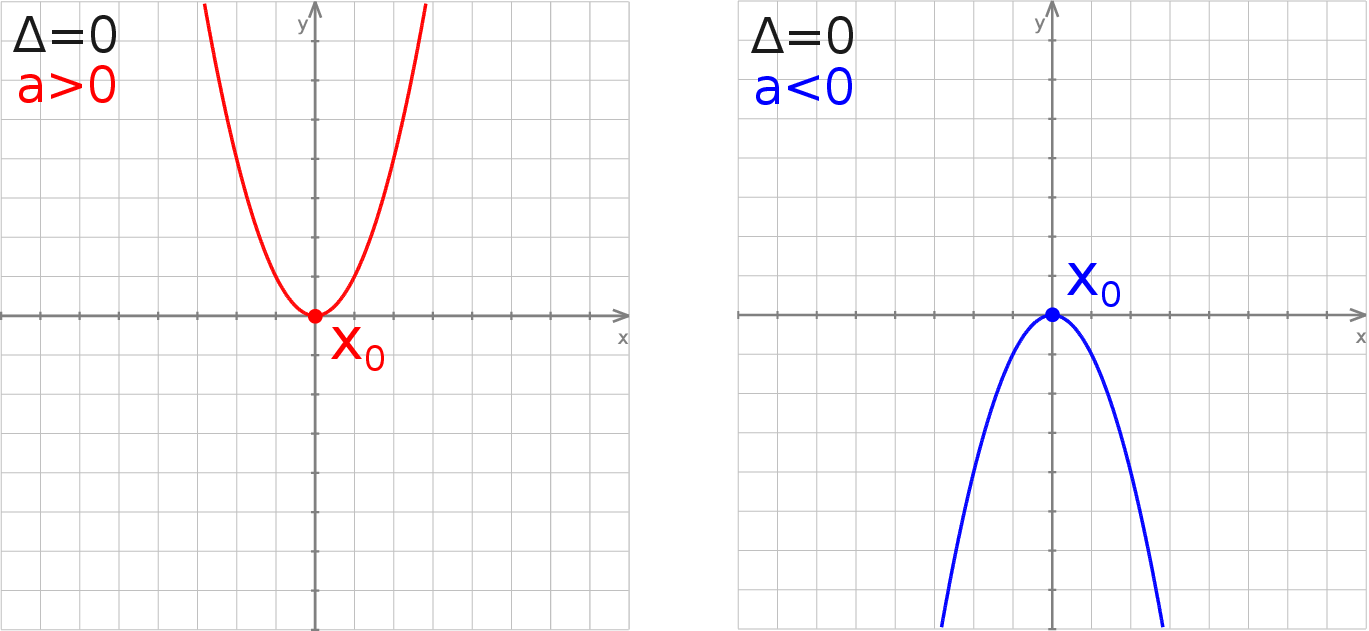
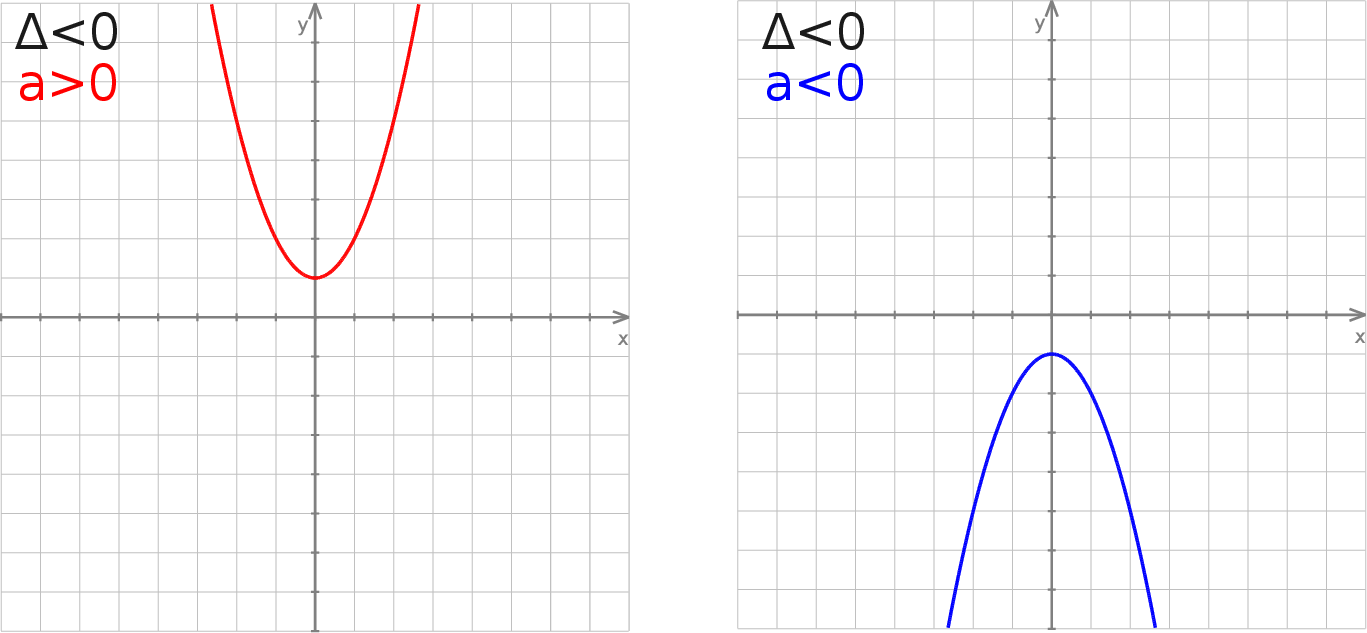
    ZINFO-FIGURE

  • Jeżeli równanie nie ma rozwiązań (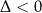Δ < 0 ) to parabola nie przecina osi Ox .

    ZINFO-FIGURE

Wierzchołek paraboli Współrzędne wierzchołka paraboli wyznacza się z tak zwanej postaci kanonicznej funkcji kwadratowej i są one równe

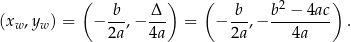
( b Δ ) ( b b2 − 4ac ) (xw,yw ) = − --,− --- = − --,− --------- . 2a 4a 2a 4a

Postać kanoniczna Sprowadzanie funkcji kwadratowej do postaci kanonicznej

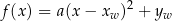
f(x ) = a(x − xw )2 + yw

bywa bardzo użyteczne i dlatego warto nauczyć się to robić.

Sprowadzenie takie wykonujemy uzupełniając do pełnego kwadratu.

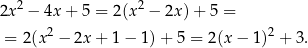
2x2 − 4x + 5 = 2 (x2 − 2x)+ 5 = 2 2 = 2(x − 2x + 1 − 1) + 5 = 2 (x− 1) + 3 .

Mając postać kanoniczną, mamy współrzędne wierzchołka: 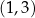(1 ,3) – dokładnie w ten sposób wyprowadza się wzory na (xw ,yw) .

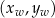Postać kanoniczna bywa natomiast bardzo użyteczna, gdy chcemy napisać wzór paraboli znając współrzędne jej wierzchołka.

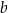Wyznacz współczynniki a i b funkcji kwadratowej 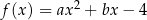2 f(x) = ax + bx − 4 jeżeli jej wierzchołek ma współrzędne (1 ,− 1) .
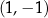Skoro znamy wierzchołek paraboli, to wiemy, że funkcja jest postaci

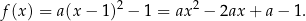
f(x) = a(x− 1)2 − 1 = ax2 − 2ax + a − 1.

Porównując współczynniki z podanym w treści zadania wzorem dostajemy 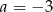a = −3 i b = 6 .

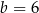Monotoniczność Każda funkcja kwadratowa ma dwa (maksymalne) przedziały monotoniczności:

  • na lewo od wierzchołka (czyli w przedziale 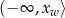(− ∞ ,xw⟩ ) jest malejąca dla 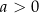a > 0 (rosnąca dla a < 0 );

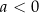  • na prawo od wierzchołka (czyli w przedziale 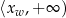⟨xw ,+ ∞ ) ) jest rosnąca dla 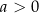a > 0 (malejąca dla a < 0 ).

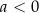Jeżeli ktoś nie pamięta, to funkcja jest rosnąca, gdy dla coraz większych argumentów przyjmuje coraz większe wartości, a malejąca, gdy przyjmowane wartości są coraz mniejsze. Na wykresie przejawia się to tym, że wykres jedzie do góry lub na dół odpowiednio (patrząc w kierunku strzałki na osi 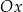Ox ).

Tips & Tricks

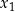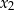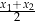1Jeżeli znamy miejsca zerowe x1 i x2 paraboli to wierzchołek znajduje się dokładnie pomiędzy nimi – jego pierwsza współrzędna jest równa x1+x2 2 .

W jakim punkcie jest wierzchołek paraboli

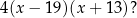
4(x− 19)(x + 13)?

Dokładnie w środku między pierwiastkami 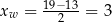xw = 19−213 = 3 .

2Jeżeli ktoś nie boi się pochodnych, to pierwsza współrzędna wierzchołka paraboli to po prostu miejsce zerowe pochodnej.

3Druga współrzędna wierzchołka paraboli to po prostu wartość funkcji kwadratowej na pierwszej współrzędnej wierzchołka – jeżeli znamy już 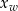xw to często łatwiej jest policzyć 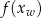f(xw ) niż wyliczać ze wzoru 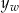yw ; tak jest na przykład dla 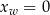xw = 0 lub xw = ± 1 .

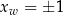Jaka jest druga współrzędna wierzchołka paraboli

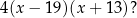
4(x− 19)(x + 13)?

Policzyliśmy już, że wierzchołek jest w punkcie 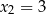x = 3 2 . Zatem

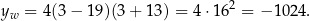
2 yw = 4 (3− 1 9)(3+ 13) = 4 ⋅16 = − 102 4.

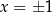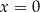4Jeżeli chcemy narysować parabolę o danym wzorze to najważniejsze jest wyznaczenie współrzędnych wierzchołka. Potem wystarczy znaleźć 1 lub 2 punkty na paraboli (np. podstawiając x = ±1 lub x = 0 ) i już możemy naszkicować parabolę. Jeżeli 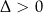Δ > 0 to wygodnie jest też znać pierwiastki. Rysując parabolę należy pamiętać o tym, że jest ona symetryczna względem pionowej prostej przechodzącej przez wierzchołek.

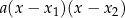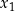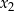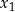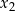5Należy pamiętać, że miejsca zerowe paraboli nie wyznaczają jej jednoznacznie – każda parabola postaci a (x− x1)(x− x2) ma miejsca zerowe x 1 i x 2 . Z tą uwagą wiąże się popularny błąd: jeżeli podane są miejsca zerowe x 1 i x 2 funkcji kwadratowej to wiele osób wnioskuje, że funkcja musi być postaci 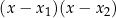(x − x 1)(x − x2) . Tymczasem może to być dowolna parabola postaci 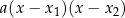a(x − x 1)(x− x2) – współczynnik a trzeba wyznaczyć z innych danych z treści zadania.

Wyznaczmy wszystkie parabole przechodzące przez punkty 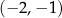(− 2,− 1) i (3 ,− 1 ) .
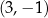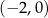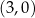Zauważmy, że jeżeli przesuniemy szukaną parabolę o 1 jednostkę do góry, to będziemy mieli parabolę o miejscach zerowych (−2 ,0) i (3,0) . Zatem szukane parabole są postaci

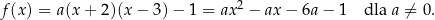
f(x ) = a(x + 2)(x − 3) − 1 = ax 2 − ax − 6a− 1 dla a ⁄= 0.

6Znając przedziały monotoniczności funkcji kwadratowej, znamy pierwszą współrzędną jej wierzchołka oraz współczynnik przy 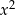x2 .

Sprawdźmy kiedy parabola

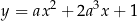
y = ax2 + 2a3x + 1

jest rosnąca na przedziale 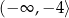(− ∞ ,− 4⟩ i malejąca na przedziale 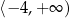⟨− 4,+ ∞ ) . Z podanych informacji wiemy, że ramiona paraboli są skierowane w dół (a < 0 ), oraz

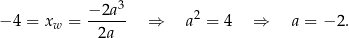
3 −-2a-- 2 − 4 = xw = 2a ⇒ a = 4 ⇒ a = − 2.

7Informacji o pierwszej współrzędnej wierzchołka paraboli dostarcza nam również znajomość jej osi symetrii.

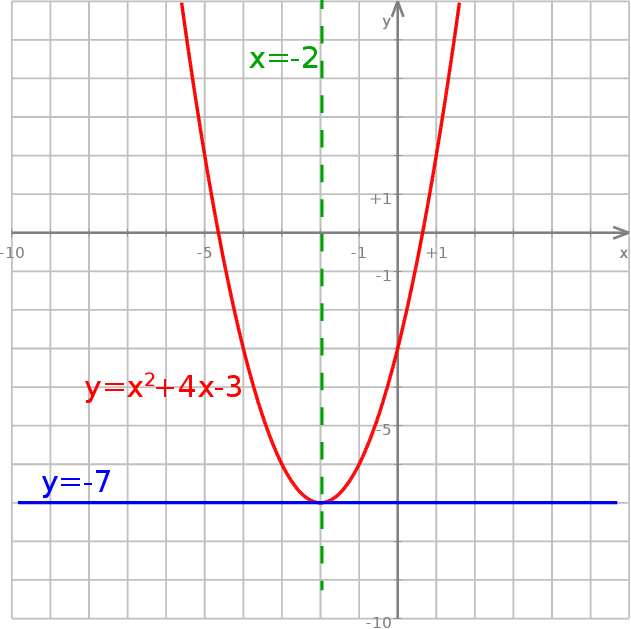
Parabola 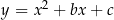y = x2 + bx + c jest symetryczna względem prostej 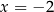x = − 2 i styczna do prostej 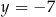y = − 7 . Wyznacz a i b .
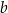Oś symetrii daje nam 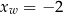xw = − 2 , czyli 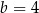b = 4 . Styczność do prostej 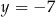y = − 7 oznacza, że druga współrzędna wierzchołka jest równa -7. Mamy więc

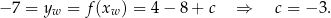
− 7 = yw = f(xw ) = 4 − 8 + c ⇒ c = − 3.

ZINFO-FIGURE

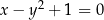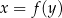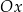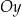8Często w zadaniach (szczególnie z geometrii analitycznej) pojawiają się równania postaci x − y2 + 1 = 0 . Aby narysować wykres takiego wyrażenia należy na nie patrzeć jak na wykres postaci x = f(y) – tzn. zamieniamy rolę osi Ox i Oy (patrzymy na kartkę z układem współrzędnych z boku).

Wykresem wyrażenia 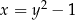x = y2 − 1 jest pozioma parabola 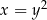x = y2 przesunięta o jedną jednostkę w lewo.

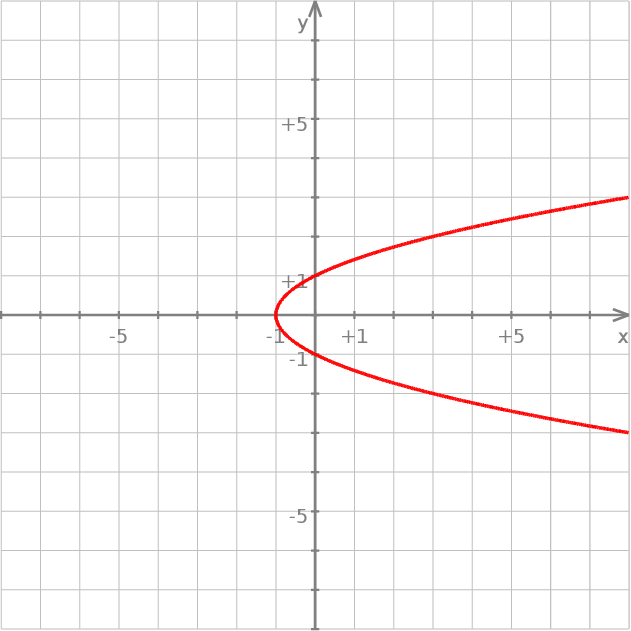
ZINFO-FIGURE

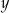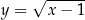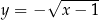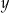Żeby było jasne, otrzymany wykres nie jest wykresem funkcji jeżeli traktujemy x –sy jako argumenty, a y –ki jako wartości – funkcja musi mieć jednoznaczną wartość dla każdego argumentu (można myśleć, że są to dwie funkcje √ ------ y = x− 1 i √ ------ y = − x − 1 narysowane w jednym układzie współrzędnych). Jest to natomiast wykres funkcji przy zamienionych rolach x –a i y –ka.

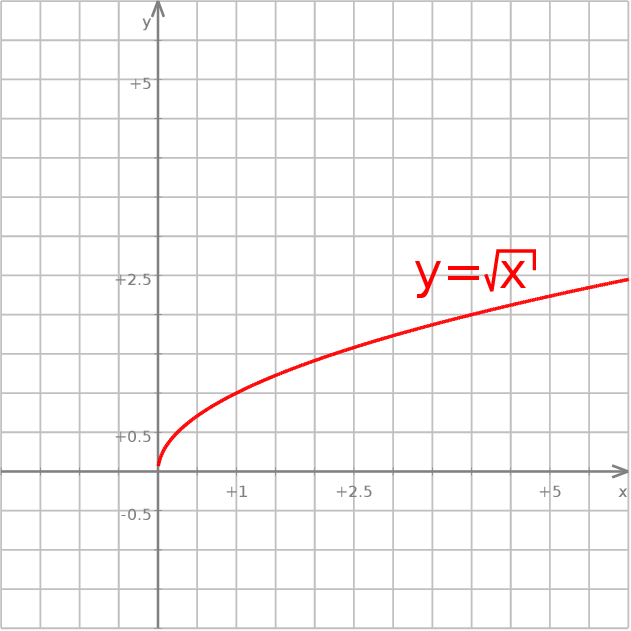
Wykresem funkcji 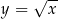√ -- y = x też jest (pozioma) parabola, a w zasadzie jej połowa. Aby to zobaczyć wystarczy przepisać sobie ten wzór w postaci 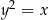y2 = x . Paraboli wychodzi pół, bo mamy założenie y ≥ 0 .

ZINFO-FIGURE

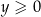9Niektóre zadania na równania/nierówności kwadratowe z parametrem sprowadzają się do ustalenia, kiedy parabola znajduje się powyżej/poniżej osi nad pewnym przedziałem.

Zastanówmy się kiedy zbiór rozwiązań nierówności

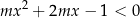
mx 2 + 2mx − 1 < 0

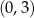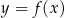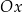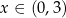zawiera przedział (0,3) . Zadanie sprowadza się do pytania kiedy parabola y = f(x) , będąca wykresem lewej strony nierówności, jest poniżej osi Ox dla x ∈ (0 ,3) . Aby odpowiedzieć na takie pytanie trzeba sobie wyobrazić wszystkie możliwe położenia takiej paraboli. W podanym przykładzie są trzy możliwości

  • Cała parabola jest poniżej osi 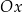Ox (współczynnik przy 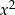2 x ujemny i Δ < 0 ).

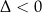  • Ramiona paraboli są skierowane w górę, ale na przedziale 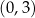(0,3) parabola jest poniżej osi (współczynnik przy 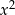x 2 jest dodatni, 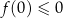f(0) ≤ 0 oraz f (3) ≤ 0 ).

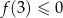  • Parabola ma ramiona skierowane w dół (współczynnik przy 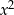2 x ujemny) i na przedziale 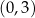(0 ,3) jest poniżej osi (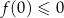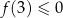f(0) ≤ 0 , f(3) ≤ 0 oraz wierzchołek musi być poza przedziałem (0,3 ) ).

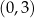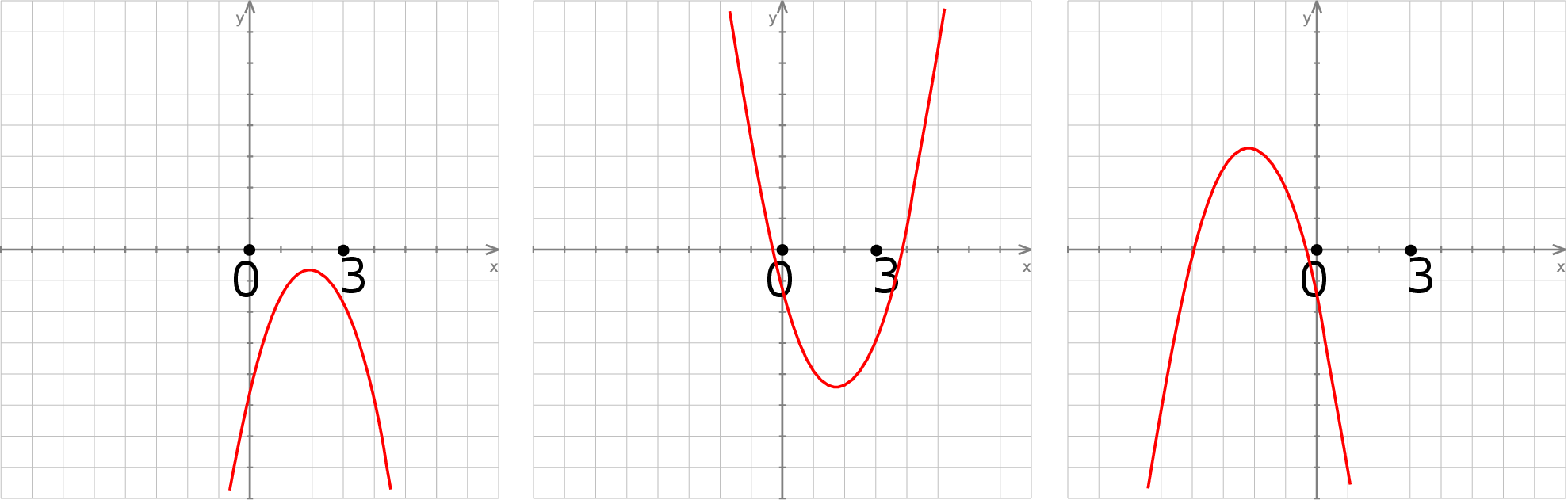
ZINFO-FIGURE

10Ile punktów wyznacza parabolę? – łatwo sobie wyobrazić, że dwa to za mało – jest pełno parabol przechodzących przez dwa punkty. Natomiast 3 punkty wyznaczają parabolę jednoznacznie – odpowiada to temu, że we wzorze funkcji y = ax 2 + bx + c mamy trzy parametry/niewiadome.

Wyznaczmy parabolę o miejscach zerowych -2 i 1 i przechodzącą przez punkt 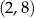(2,8) .
Z informacji o miejscach zerowych wiemy, że parabola jest postaci

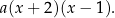
a(x + 2)(x − 1).

Z informacji o podanym punkcie wyliczamy 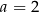a = 2 .

Od tej zasady jest jeden ważny wyjątek – parabola jest jednoznacznie wyznaczona przez wierzchołek i jeden dodatkowy punkt. Powód jest taki, że żądanie, żeby jakiś punkt był wierzchołkiem, daje dwa równania – jedno, że punkt leży na paraboli, drugie, że jest wierzchołkiem. W tego typu zadaniach bardzo wygodna jest postać kanoniczna.

Wyznaczmy parabolę przechodzącą przez punkt 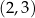(2,3) , której wierzchołek jest w punkcie 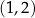(1,2) . Korzystając z postaci kanonicznej, parabola taka musi mieć postać

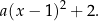
a(x − 1)2 + 2.

Uwzględniając podany punkt na paraboli otrzymujemy 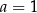a = 1 .

11W zasadzie nie ma to wiele wspólnego z zadaniami szkolnymi, ale tak jak okrąg jest zbiorem punktów, które są równo odległe od ustalonego punktu, parabola jest zbiorem punktów, które są równo odległe od ustalonej prostej (kierownicy) i punktu (ogniska).

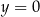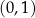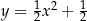Można policzyć, że dla kierownicy y = 0 i ogniska (0,1) wychodzi parabola 1 2 1 y = 2x + 2 .

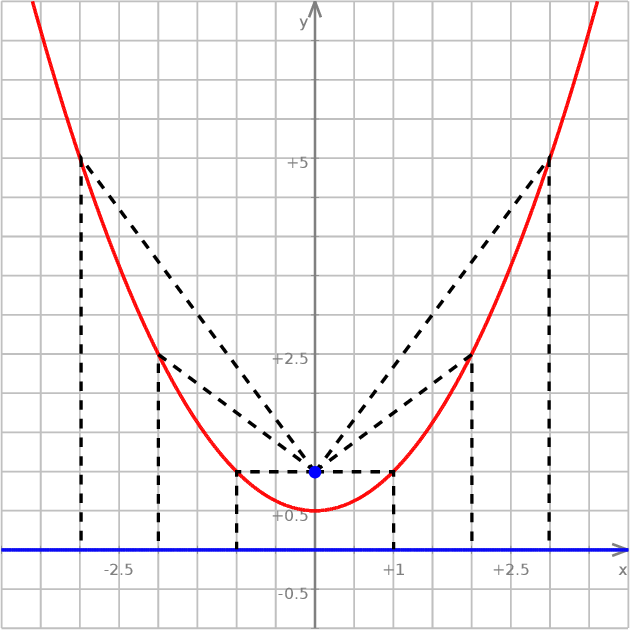
ZINFO-FIGURE

12Na początku trudno w to uwierzyć, ale wszystkie parabole mają dokładnie taki sam kształt, to znaczy każde dwie parabole różnią się o jednokładność i przesunięcie – sytuacja jest identyczna jak dla okręgów: z dokładnością do rozmiaru wszystkie są takie same.

Sprawdźmy co się stanie z parabolą 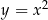y = x 2 po jednokładności o środku w 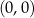(0,0) i skali 2.
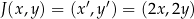Możemy tę jednokładność J zapisać następująco: J(x,y) = (x ′,y′) = (2x ,2y ) . Równanie paraboli po tej zmianie będzie miało postać

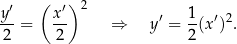
′ ( ′) 2 y- = x- ⇒ y ′ = 1(x′)2. 2 2 2

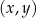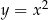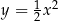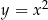(punkt (x,y) , który spełniał równanie y = x2 , po jednokładności spełnia wyprowadzone równanie). Opuszczając primy (nie ma znaczenia jakim znaczkiem oznaczamy argumenty i wartości funkcji), otrzymujemy parabolę 1 2 y = 2x – tak więc parabola ta jest dokładnie dwa razy większa od y = x2 .

ZINFO-FIGURE

Wersja PDF