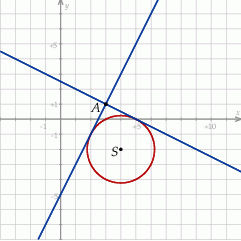
Zadanie nr 2962121
Wykaż, że styczne do okręgu 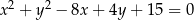 poprowadzone przez punkt
poprowadzone przez punkt 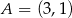 są prostopadłe.
są prostopadłe.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
Jeżeli zapiszemy równanie okręgu w postaci
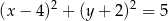
to widać, że mamy do czynienia z okręgiem o środku 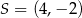 i promieniu
i promieniu 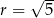 .
.
Sposób I
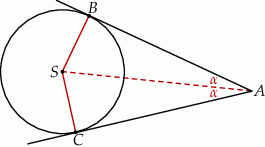
Jeżeli oznaczymy przez 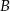 i
i 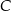 punkty styczności stycznych poprowadzonych z punktu
punkty styczności stycznych poprowadzonych z punktu 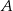 do okręgu, to
do okręgu, to
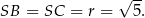
Ponadto
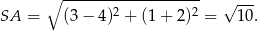
Zatem
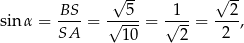
czyli 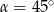 . To oznacza, że
. To oznacza, że 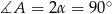 .
.
Sposób II
Tym razem użyjemy odrobinę więcej geometrii analitycznej i wyliczymy równania stycznych.
Proste przechodzące przez punkt 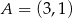 mają postać
mają postać
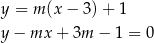
(tak naprawdę brakuje w tym pęku pionowej prostej 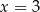 , ale łatwo sprawdzić, że nie jest ona szukaną styczną).
, ale łatwo sprawdzić, że nie jest ona szukaną styczną).
Prosta ta będzie styczna do danego okręgu jeżeli odległość środka 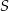 tego okręgu od tej prostej będzie równa
tego okręgu od tej prostej będzie równa 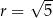 . Na mocy wzoru na odległość punktu od prostej mamy więc równanie
. Na mocy wzoru na odległość punktu od prostej mamy więc równanie
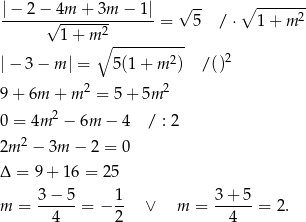
Teraz wystarczy zauważyć, że iloczyn współczynników kierunkowych otrzymanych prostych jest równy 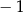 , więc proste te są prostopadłe.
, więc proste te są prostopadłe.
Na koniec obrazek dla ciekawskich.